Die Allgemeinen Transformatorformeln

ID: 402448

Die Allgemeinen Transformatorformeln

08.Aug.16 21:18

5023

Jochen Bauer (D)
Redakteur
Beiträge: 126
Anzahl Danke: 14

Transformatoren finden in der Radiotechnik in allen Frequenzbereichen vielfältige Verwendung, sei es als Netztransformator, Tontransformator oder Hochfrequenzübertrager. Aber auch Anwendungen wie die induktive Antennenankopplung oder induktiv gekoppelte ZF-Bandfilter laufen von der Berechnung her stets auf die allgemeinen Transformatorformeln hinaus. Diese sollen daher hier kurz hergeleitet und anschließend näher betrachtet werden.

Wir gehen von der folgenden Transformatorschaltung aus:

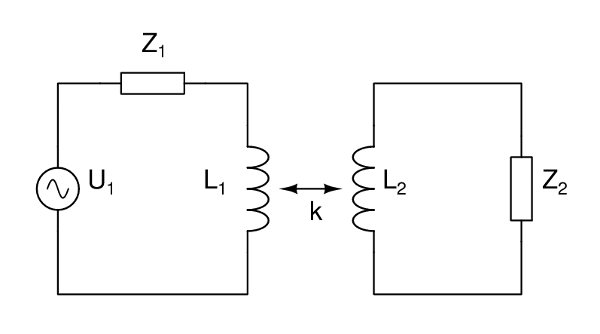
Bei dieser sehr allgemeinen Transformatorschaltung wird die Primärseite (links) von einer idealen Spannungsquelle U₁ in Reihe mit einer (im allgemeinen komplexen) Impedanz Z₁ angetrieben. Die primärseitige Induktivität L₁ ist magnetisch mit der sekundärseitigen Induktivität L₂ gekoppelt. Der Kopplungsfaktor k ist dabei eine reelle Zahl zwischen -1 und +1, wobei das Vorzeichen durch den gegenseitigen Windungssinn von Primär- und Sekundärspule bestimmt wird. Für |k|=1 sind Primär- und
Sekundärseite vollständig gekoppelt. Die (in der Praxis natürlich nur näherungsweise erreichbare) vollständige Kopplung findet bei Netz- und Tontransformatoren Anwendung. Bei der Antennenkopplung und bei Bandfiltern ist k deutlich niedriger und liegt typischerweise in der Größenordnung von k=0.01 bis k=0.2 Auf der Sekundärseite befindet sich eine (im allgemeinen wieder komplexe) Impedanz Z₂.

Die Kirchhoffsche Maschenregel für komplexe Spannungen [1] besagt, dass sich die Spannungen an den Komponenten der Primärseite zur Antriebsspannung U₁ aufaddieren, wir haben also

$I_1 Z_1+U_{\scriptscriptstyle L1}=U_1 \hspace{33pt}(1)$

wobei I₁ der komplexe Strom im Primärkreis ist. Da im Sekundärkreis keine Spannungsquelle vorhanden ist, addieren sich hier die Spannungen an den Komponenten zu Null auf. Es ist also

$I_2 Z_2+U_{\scriptscriptstyle L2}=0 \hspace{33pt}(2)$

Die Klemmspannungen U_L1 bzw. U_L2 an dem Induktivitäten L₁ und L₂ sind nach dem Induktionsgesetz [2] durch

$U_{\scriptscriptstyle L1}=I_1\cdot j\omega L_1-I_2\cdot j\omega M \hspace{33pt}(3)$

sowie

$U_{\scriptscriptstyle L2}=I_2\cdot j\omega L_2-I_1\cdot j\omega M \hspace{33pt}(4)$

gegeben. Dabei ist M die gegenseitige Induktivität (engl. mutual inductance) die sich aus L₁, L₂ und dem Kopplungsfaktor k gemäß [2]

$M=k\cdot\sqrt{L_1 L_2}$

berechnet. Damit erhält man aus den Gleichungen (1) und (2) unmittelbar

$I_1 Z_1+I_1\cdot j\omega L_1-I_2\cdot j\omega M=U_1 \hspace{33pt}(5)$

und

$I_2 Z_2+I_2\cdot j\omega L_2-I_1\cdot j\omega M=0 \hspace{33pt}(6)$

Nach einigen Umformungen gewinnt man daraus die Gleichungen

$I_1\cdot(Z_1+j\omega L_1+Z_{21})=U_1 \hspace{33pt}(7)$

$I_2\cdot(Z_2+j\omega L_2+Z_{12})=U_{12} \hspace{33pt}(8)$

mit

$Z_{21}=\frac{(\omega M)^2}{Z_2+j\omega L_2} \hspace{33pt}(\mathrm{T}1)$

und

$Z_{12}=\frac{(\omega M)^2}{Z_1+j\omega L_1} \hspace{33pt}(\mathrm{T}2)$

Wie sind diese beiden Gleichungen nun zu interpretieren? Gleichung (7) stellt offensichtlich den Zusammenhang zwischen dem komplexen Strom I₁ und der Antriebsspannung U₁ im Primärkreis gemäß dem komplexen Ohmschen Gesetz her. Damit folgt natürlich sofort, dass Z₂₁ eine vom Sekundärkreis in den Primärkreis eingekoppelte komplexe Impedanz ist, die in Reihe mit Z₁ liegt. Analog folgt aus Gleichung (8), dass Z₁₂ eine vom Primärkreis in den Sekundärkreis eingekoppelte komplexe Impedanz ist, die in Reihe mit Z₂ liegt. Außerdem ist U₁₂ offensichtlich die vom Primärkreis in den Sekundärkreis eingekoppelte Antriebsspannung.

Damit lassen sich Primär- und Sekundärkreis mit Ersatzschaltungen gemäß der folgenden Abbildung darstellen:

Dabei ist zu beachten, dass in diesem Ersatzschaltbild keine induktive Kopplung mehr zwischen L₁ und L₂ vorhanden ist. Die Auswirkungen der Kopplung in der ursprünglichen Schaltung werden vollständig durch Z₂₁, Z₁₂ und U₁₂ beschreiben.

Zusätzlich zu den Gleichungen (7) und (8) lassen sich aus den Ausgangsgleichungen durch weitere Umformungen noch die Gleichungen

$U_{12}=\frac{j\omega M}{Z_1+j\omega L_1}U_1 \hspace{33pt}(\mathrm{T}3)$

und

$I_2=\frac{i\omega M}{Z_2+j\omega L_2}I_1 \hspace{33pt}(\mathrm{T}4)$

gewinnen, die das Verhältnis der komplexen Ströme bzw. Spannungen zwischen Primär- und Sekundärseite beschreiben.

Die Gleichungen (T1) bis (T4) beschreiben zusammen mit dem Ersatzschaltbild den Transformator vollständig und können als allgemeine Transformatorformeln bezeichnet werden.

Zur weiteren Betrachtung ist es nun zweckmäßig, die komplexen Impedanzen Z₁ und Z₂ auf der Primär- bzw. Sekundärseite in den Ohmschen- und Blindanteil (mathematisch gesehen also in Real- und Imaginärteil) gemäß

$Z_1=R_1+j X_1 \hspace{11pt}\mathrm{und}\hspace{11pt} Z_2=R_2+j X_2$

aufzuteilen. Man erhält damit aus den Gleichungen (T1) und (T2) nach Auftrennung in Real- und Imaginärteil

$Z_{21}=\frac{(\omega M)^2}{R^2_2+(\omega L_2+X_2)^2}\cdot\Big(R_2-j(\omega L_2+X_2)\Big) \hspace{33pt}(9)$

und

$Z_{12}=\frac{(\omega M)^2}{R^2_1+(\omega L_1+X_1)^2}\cdot\Big(R_1-j(\omega L_1+X_1)\Big) \hspace{33pt}(10)$

Aus den Gleichung (T3) und (T4) ergibt sich

$U_{12}=U_1\cdot\frac{\omega M}{R^2_1+(\omega L_1+X_1)^2}\cdot\Big(\omega L_1+X_1+j R_1\Big) \hspace{33pt}(11)$

sowie

$I_2=I_1\cdot\frac{\omega M}{R^2_2+(\omega L_2+X_2)^2}\cdot\Big(\omega L_2+X_2+j R_2\Big) \hspace{33pt}(12)$

und daraus für das Verhältnis der Beträge der Ströme und Spannungen

$\lvert U_{12}\rvert=\lvert U_1\rvert\cdot\frac{\omega M}{\sqrt{R^2_1+(\omega L_1+X_1)^2}} \hspace{33pt}(11\mathrm{a})$

und

$\lvert I_2\rvert=\lvert I_1\rvert\cdot\frac{\omega M}{\sqrt{R^2_2+(\omega L_2+X_2)^2}} \hspace{33pt}(12\mathrm{a})$

Dies sieht nun alles zunächst in keinster Weise nach den "einfachen Transformatorgleichungen" aus, die einem im Schulunterricht oder der Ausbildung begegnet sind. Das liegt daran, das sich diese nur auf den häufig vorkommenden Fall mit X₁=X₂=0 beziehen, außerdem die Induktivitäten L₁ und L₂ so hoch sind, dass

$R^2_1+(\omega L_1)^2\approx (\omega L_1)^2 \hspace{11pt}\mathrm{und}\hspace{11pt} R^2_2+(\omega L_2)^2\approx (\omega L_2)^2$

für alle vorkommenden Antriebsfrequenzen ω gilt und die Kopplung von Primär- und Sekundärseite näherungsweise vollständig ist, also (bei positivem Vorzeichen von k)

$k\approx 1 \hspace{11pt}\mathrm{bzw.}\hspace{11pt} M\approx\sqrt{L_1 L_2}$

gilt. In diesem Fall vereinfachen sich die Gleichungen (9), (10), (11a) und (12a) sofort zu

$\frac{\lvert U_{12}\rvert}{\lvert U_1\rvert} \approx \sqrt{\frac{L_2}{L_1}} \hspace{66pt}(13)$

$\frac{\lvert I_2\rvert}{\lvert I_1\rvert} \approx \sqrt{\frac{L_1}{L_2}} \hspace{73pt}(14)$

$Z_{21}\approx R_2\cdot\frac{L_1}{L_2}-j\omega L_1 \hspace{33pt}(15)$

$Z_{12}\approx R_1\cdot\frac{L_2}{L_1}-j\omega L_2 \hspace{33pt}(16)$

Die Gleichungen (13) und (14) sind direkt die altbekannten "einfachen Transformatorgleichungen" für das Verhältnis der Ströme und Spannungen. Aus den Gleichungen (15) und (16) lässt sich folgern, dass das induktive Verhalten der Primär- bzw. Sekundärspule durch den in den Primär- bzw. Sekundärkreis eingekoppelten Blindwiderstand -jωL₁ bzw. -jωL₂ vollständig aufgehoben wird und eine Übersetzung der Ohmschen Widerstände gemäß

$\frac{R_2}{R_1}=\frac{L_2}{L_1}$

statt findet.

[1] de.wikipedia.org/wiki/Kirchhoffsche_Regeln

[2] en.wikipedia.org/wiki/Inductance

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.