Leistungs- und Spannungs-Pegel; Dezibel, Dämpfung
Leistungs- und Spannungs-Pegel; Dezibel, Dämpfung

In der Nachrichtentechnik ist es üblich, mit Pegeln zu rechnen. Hierfür gibt es zwei Gründe:
- Verstärkungen und Dämpfungen haben oft große Zahlenwerte.
- Multiplikationen bzw. Divisionen reduzieren sich auf Additionen bzw. Subtraktionen.
Bei zwei Übertragungs-Blöcken (z.B. Vor-Verstärker und Leistungs-Verstärker mit den Verstärkungen VV bzw. VH ), die in Kette (hinter einander) geschaltet sind, gilt für die Gesamt-Verstärkung VG, daß diese das Produkt VG = VV·VH ist.
Rechnet man mit Pegelwerten, wird aus dem Produkt eine Addition pG = pV + pH. Da Addition einfacher ist als Multiplikation, speziell auch mit großen Zahlenwerten, wird also das Rechnen mit Pegeln in der Praxis bevorzugt.
Die Zusammenhänge
Will man mit den Pegel richtig rechnen, muß man die Zusammenhänge zwischen den Zahlenwerten und diesen Pegeln kennen.
Von den Zahlenwerten zu den Pegeln gelangt man über einen Logarithmus. Der Hintergrund dazu ist, daß sich jeder Zahlenwert in Exponenten-Schreibweise, bezogen auf eine Basiszahl, darstellen läßt.
Üblich ist als Basiszahl den Wert 10 zu nehmen, was im weiteren Verlauf auf das „Dezibel“ führen wird.
| Zahl | 10 | 100 | 1000 | 10000 |
| Exp-Schreibweise | 101 | 102 | 103 | 104 |
Hier gibt also der Exponent einfach die Anzahl der Nullen nach der 1 an.
Für die Werte gilt: 10000 = 100·100. Für die Exponenten gilt: 4 = 2+2.
Diese Exponentenschreibweise beschränkt sich jedoch nicht nur auf so „glatte“ Zahlen wie in diesem Beispiel. Mathematisch kann jede Zahl in Exponentenschreibweise dargestellt werden. Dann sind die Exponenten allerdings keine ganzen Zahlen mehr. Es mag vielleicht schwierig sein, sich z.B. 0,35 Nullen vorzustellen, aber mathematisch ist das kein Problem. Man kann das genau so einfach berechnen. (Werte mit Taschenrechner)
| Zahl | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Exp-Schr. | 100 | 100,301 | 100,4771 | 100,602 | 100,699 | 100,778 | 100,845 | 100,903 | 100,9542 |
Rechnet man nur mit den Exponenten, so hat man mathematisch den Logarithmus (log) gebildet. In diesem Fall ist das der Logarithmus zur „Basis“ 10, der als "log10" oder "lg" geschrieben wird.
Beim Logarithmus muß also immer dazu gesagt werden, zu welcher Basis-Zahl dieser Exponent gehört, damit man den richtigen Zahlenwert damit berechnen kann.
Da z.B. 0,1 =1/10 = 1/101 = 10-1 ist, kann man allgemein schreiben log(1/x) = -log(x). Damit reduziert sich eine Division der Zahlenwerte zur Subtraktion der Logarithmen.
Dezibel
Die Logarithmen zur Basis 10 (log10 bzw. lg) ergeben kleine Werte, wie der Tabelle zu entnehmen ist. Zum bequemeren Rechnen nimmt man daher immer den 10 fachen Wert 10·log10 . Diese Werte werden mit „Dezi-Bel“ (dB) bezeichnet. Das dB ist eine „Pseudo-Einheit“ und weist auf die verwendete Basiszahl 10 hin.
Neper
In der älteren Literatur wird meist e = 2,718281828.... als Basiszahl verwendet. Mit der Zahl „e“ wird das natürliche Wachstum beschrieben. Die entsprechende Hochzahl (Exponent) wird dann mit „Neper“ (Np) bezeichnet. Der so gebildete „natürliche“ Logarithmus wird als loge = ln geschrieben.
Für die Umrechnung gilt 1dB = 0,1151Np oder 1Np = 8,686dB
Nomogramm zur Umrechnung von Neper <=> Dezibel

Zahlen mit Einheiten
In der Technik hat man keine reinen Zahlen, sondern diese sind immer in Verbindung mit einer Einheit, also „Größen“, wie z.B. 100mW oder 5V oder 30mA. Was ist aber der Logarithmus von einer Einheit?
Man behilft sich dabei so, daß die Größen durch entsprechende „Bezugsgrößen“ dividiert werden. Also z.B. 100mW/1mW = 100 oder 5V/1V = 5 oder 30mA/1mA = 30.
Wählt man willkürliche Bezugsgrößen, bezeichnet man die Pegel als „relativ“.
Wählt man vereinbarte Bezugsgrößen, bezeichnet man die Pegel als „absolut“.
Das dB ist auf Leistungen P bezogen, folglich gilt für den Leistungs-Pegel pp:
pp = 10lg(P/P0), wobei P0 die „Bezugs-Leistung“ ist.
Nun gilt aber bekanntlich P = U·I = U2/Z = I2·Z , wobei Z der Widerstand ist, in dem die Leistung umgesetzt wird.
Wird nun der Spannungs-Pegel pu gebildet, so gilt (gleicher Wert für Z vorausgesetzt):
pu = 10lg({U2/Z}/{U02/Z}) = 20lg(U/U0) ;
Eine Hochzahl, hier die 2, wird nach dem Logarithmieren ein multiplikativer Faktor, so daß aus dann aus 10lg( ) nun 20lg( ) wird.
Merke: Für Leistungs-Pegel gilt 10lg( ); für Spannungs-Pegel gilt 20lg( )
Die folgende Tabelle zeigt weitere Einzelheiten. Hier wird auch berücksichtigt, wenn bei der Umrechnung von Leistung auf Spannung unterschiedliche Werte Z bzw. Z0 vorhanden sind.

Beispiele für Pegelangaben:

Beipiele für einen absoluten Pegel

Man erkennt: Leistungs-Erhöhung ergibt positiven Pegel, während Leistungs-Verminderung negativen Pegel ergibt.
Einige Beispiele für Spannungs- und Leistungs-Werte als Pegel

Man sieht hier, daß die Spannungs-Verhältnisse und die Leistungs-Verhältnisse unterschiedliche Zahlenwerte für den gleichen dB Wert haben. Da aber die Leistung proportional zur Spannung im Quadrat ist, stimmen die beiden Zahlenwerte damit doch wieder überein.
Wenn nun die Quelle (Pegel-Sender) und der Verbraucher ungleiche Widerstände Z0 bzw. Z haben, muß das beim Übergang vom Leistungs-Pegel zum Spannungs-Pegel berücksichtigt werden. (In der Nachrichtentechnik haben die Pegelsender meist Z0= 600Ω Innenwiderstand.)

Dämpfung
Dämpfung ist Abschwächung und damit das Gegenteil von Verstärkung, also
Dämpfung = 1/Verstärkung.
- Bezieht man dB auf Verstärkung, so bedeuten positive dB Werte eine Verstärkung, während negative dB Werte eine Dämpfung bedeuten.
Wird nur mit Dämpfungen gearbeitet, spart man sich das negative Vorzeichen dadurch ein, daß man den Quotienten P/P0 durch den reziproken Quotienten P0/P ersetzt. Dadurch werden alle "Dämpfungs-dBs" nun positiv.
- Bezieht man dB auf die Dämpfung, so sind positive dB Werte eine Dämpfung, während negative dB Werte eine Verstärkung bedeuten.
Die Tabelle zeigt die Definitionen der verschiedenen Dämpfungen.

Daß Verstärkung und Dämpfung reziprok zu einander sind - und folglich die entsprechenden dB Werte ihr Vorzeichen wechseln - ist "eine böse Falle" für jeden der mit der Rechnung mit dBs schlampig umgeht.
Für Übertragungs-Strecken ist es üblich "Pegel-Pläne" (eigentlich: Dämpfungs-Pläne) anzugeben.

An der Skala links ist auch zu sehen, daß Pegel/dB und Dämpfung/dB ein unterschiedliches Vorzeichen haben.
Am Bezugspunkt P0 wird der relative Pegel 0dB angenommen. Wenn der Pegelsender hier einen anderen Pegel liefert, ist das für eine Messung kein Problem, weil sich das ja leicht umrechnen läßt, wie das folgende Beispiel zeigt. Man bezeichnet dann den Pegel am Bezugspunkt mit dBr (relativer Pegel).

Lit:
Schuon, E.; Wolf, H.: Nachrichten-Meßtechnik, Springer, 1981
Wandel & Goltermann: Nachrichtenübertragungstechnik, Firmendruckschrift. o.J.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
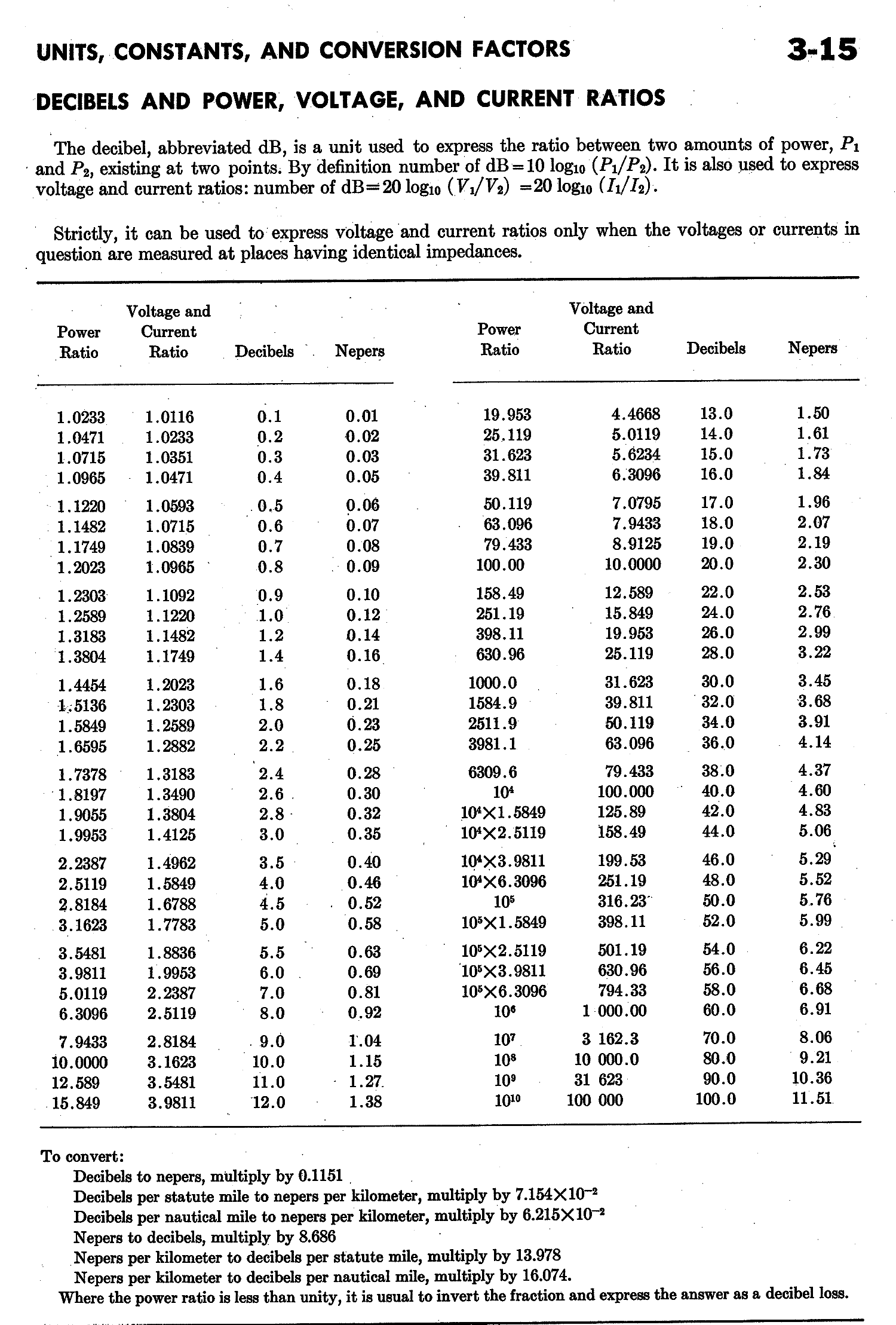
Umrechnungstabelle Dezibel <==> Neper

Im ITT Handbuch, 6.A., Sams, 1975 gibt es eine Umrechnungstabelle zwischen Dezibel und Neper.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.