Die Frequenzabhängigkeit der Lautsprecherimpedanz
Die Frequenzabhängigkeit der Lautsprecherimpedanz

Die "Impedanz" eines Lautsprechers wird meistens als nomineller Wert in Form eines Ohmschen Widerstandes angegeben, typische Werte sind 4Ω ,8Ω und 16Ω. Die tatsächliche Impedanz eines Lautsprechers ist jedoch wie allgemein bekannt frequenzabhängig und ergibt sich aus den Eigenschaften des Lautsprechers als gekoppeltes mechanisch-elektrisches System. Betrachten wir daher zunächst den grundlegenden Aufbau eines einfachen Lautsprechers mit Permanentmagnet wie in der folgenden Skizze gezeigt.

Das bekannte Grundprinzip ist relativ einfach. Eine vom NF-Wechselstrom durchflossene Spule erfährt im Magnetfeld des Permanentmagneten eine Lorentzkraft [1], die die Membran bewegt und damit das elektrische NF-Signal in Schallwellen umwandelt. Für die Berechnung der elektrischen Impedanz zwischen den Anschlüssen der Spule ist nun diese Bewegung der Membran wesentlich.
Die Membran kann in erster Näherung als angetriebener, verlustbehafteter harmonischer Oszillator beschreiben werden. Die Antriebskraft ist dabei die Kraft auf die von einem zeitabhängigen Strom I(t) durchflossene Lautsprecherspule mit einer gesamten Leiterlänge (Umfang x Windungszahl) von l im radialen Magnetfeld des Permanentmagneten mit der Flußdichte B (siehe obige Skizze). Geht man von einem ausschließlich radialen Magnetfeld parallel zur Spulenebene aus, so ergibt sich diese aus der Lorentzkraft zu [1]
Die Lorentzkraft ist dabei senkrecht zur Spulenebene und zum radialen Magnetfeld. Sie bewegt also wie erwartet die Membran entlang der Achse des Lautsprechers. Die Bewegungsgleichung für die Auslenkung x(t) der Membran ist damit [2]
Dabei ist m die Masse der Schwingspule und der Membran, r der mechanische Verlustwiderstand des Oszillators der die Dissipation von Schwingungsenergie in der Membran und die Abstrahlung von Schallwellen in den Raum beschreibt und s die Federkonstante des Oszillators die sich aus der elastischen Eigenschaft der Membran und der Kompression der Luft im Lautsprechergehäuse bei der Bewegung der Membran ergibt.
Wir müssen nun den Zusammenhang zwischen dem Strom I(t) in der Lautsprecherspule und der dafür notwendigen Klemmenspannung U(t) finden. Würde sich die Membran und damit die Spule im Magnetfeld nicht bewegen, so wäre diese einfach durch den Ohmschen Widerstand und die Induktivität der Spule gemäß
gegeben. Durch die Bewegung der Spule im Magnetfeld kommt nun aber noch eine mechanisch-elektrische Rückwirkung hinzu, da in der im Magnetfeld bewegten Spule wiederum eine Spannung induziert wird. Diese wird über die Lorentzkraft auf die Elektronen in der Leiterschleife berechnet [3] und ergibt sich unter Annahme eines ausschließlich radialen Magnetfeldes zu [3] Umer=Blv, wobei v die Geschwindigkeit der Lautsprecherspule im Magnetfeld ist. Es ergibt sich damit eine gesamte Klemmspannung von
Mit dem komplexwertigen Ansatz
für sinusförmige Spannungen, Ströme und Auslenkungen ergibt sich aus Gleichung (1) sofort
was in Gleichung (2) eingesetzt zu
mit einer Lautsprecherimpedanz Z von
führt. Zur weiteren Diskussion ist es sinnvoll diese ihren Ohmschen Anteil (Realteil) und Blindanteil
(Imaginärteil) gemäß
zu zerlegen. Der Ohmsche Anteil besteht aus dem elektrischen Ohmschen Widerstand R der Spule und einem Term der aus den mechanischen Verlusten und der mechanisch-elektrischen Rückwirkung des Systems erwächst. Diese Verluste sind offensichtlich bei der mechanischen Resonanz des Lautsprechers bei
am größten. Der Blindanteil besteht aus dem induktiven Widerstand der Lautsprecherspule und ebenfalls einem Term der aus der mechanisch-elektrischen Rückwirkung des Systems entsteht. Dieser Blindanteil der mechanisch-elektrischen Rückwirkung verschwindet offensichtlich im Falle der mechanischen Resonanz des Lautsprechers. Unterhalb der mechanischen Resonanzfrequenz des Lautsprechers ist dieser Anteil induktiv und ändert am mechanischen Resonanzpunkt sein Vorzeichen zu einem kapazitiven Verhalten. Für hinreichend hohe Frequenzen dominiert natürlich der induktive Widerstand der Lautsprecherspule.
Die Parameter m, s und r des Lautsprechers als verlustbehafteter harmonischer Oszillator können näherungsweise mit den Thiele-Small Parametern [4] Mms, 1/Cms und Rms gleich gesetzt werden. Das Produkt Bl ist ebenfalls einer der Thiele-Small Parameter. Diese Parameter werden für viele (meistens höherwertige) Lautsprecher aus moderner Produktion von den Herstellern angegeben. Wir können damit die Impedanzkurve Z eines beispielhaften Lautsprechers berechnen und plotten. Für alle folgenden Diagramme wurden die Parameter R=7.9Ω, L=300μH, Bl=4Tm, m=4g, s=1200N/m und r=0.6Ns/m verwendet.
Betrachten wir zunächst den Verlauf des Betrages der Lautsprecherimpedanz |Z|. Diese ist für den
Frequenzbereich von 10Hz bis 10kHz im Diagramm unten dargestellt.
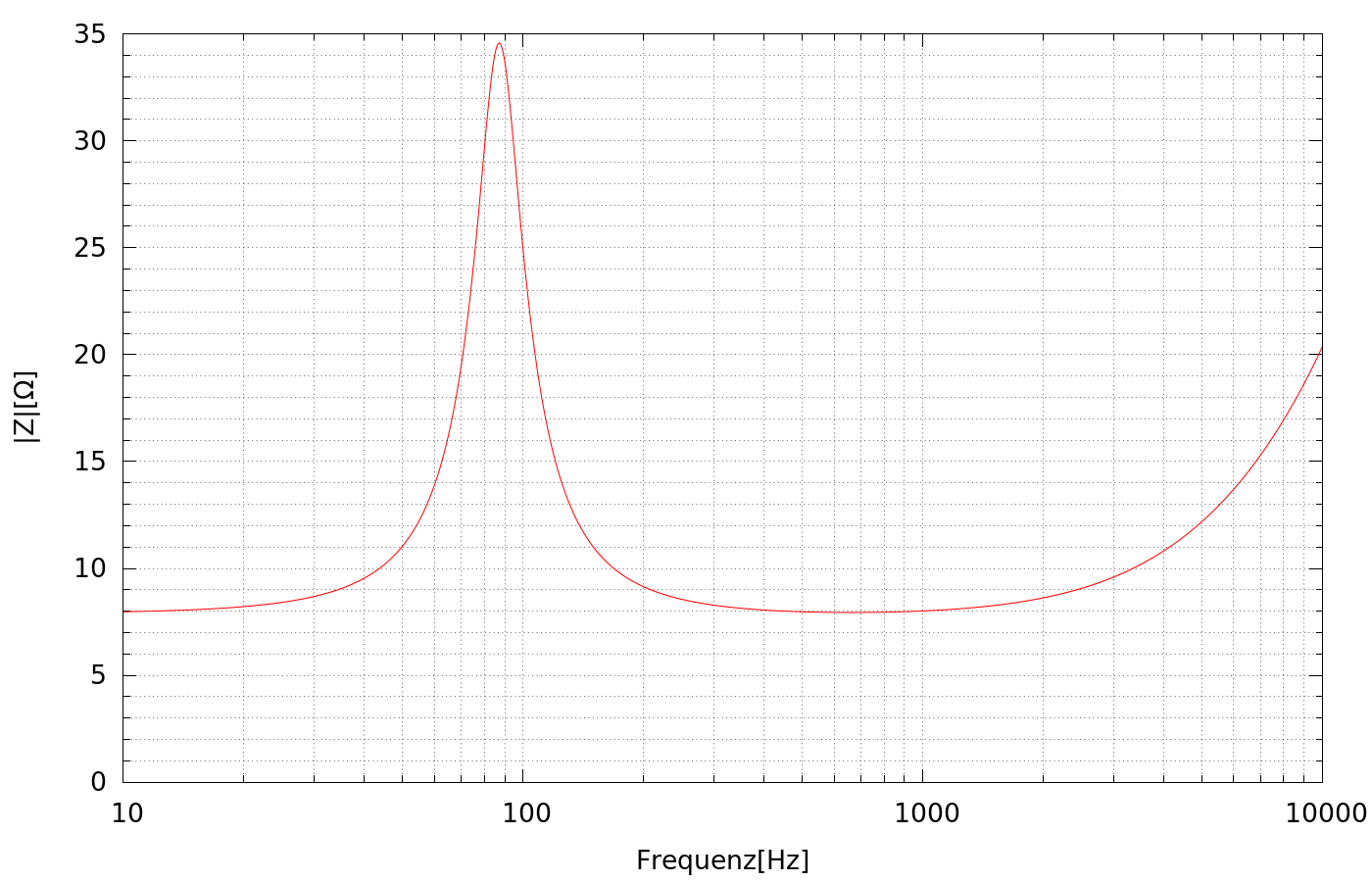
Es ist deutlich das bei der mechanischen Resonanz des Lautsprechers (ca. 87Hz) auftretende Maximum der Impedanz zu erkennen. Bei Frequenzen überhalb der mechanischen Resonanz des Lautsprechers sinkt die Impedanz dann wieder ab und bleibt in einem größeren Frequenzbereich in grober Näherung konstant bis der induktive Blindwiderstand der Lautsprecherspule merklich wird und zu einem erneuten Ansteigen der Impedanz führt.
Die getrennte Darstellung des Ohmschen- und Blindanteils ergibt folgendes Diagramm:

Auch hier ist die mechanischen Resonanz des Lautsprechers im Verlauf des Ohmschen Widerstandes deutlich zu erkennen. Auch ist der Wechsel des Blindwiderstandes von induktivem (Im(Z)>0) zu kapazitivem Verhalten (Im(Z)<0) am mechanischen Resonanzpunkt zu sehen. Ab ca. 600Hz wird der gesamte Blindwiderstand aufgrund des ansteigenden induktiven Blindwiderstandes der Lautsprecherspule insgesamt wieder induktiv.
In Röhrenendstufen müssen derartig niedrige Impedanzen im Ohm-Bereich durch einen NF-Übertrager auf Impedanzen typischerweise im Kiloohm Bereich herauftransformiert werden. Aus dem formelmäßigen Ausdruck für die Impedanz des Lautsprechers auf der Sekundärseite des NF-Übertragers kann mit Hilfe der allgemeinen Transformatorformeln [5] die auf der Primärseite sichtbare Impedanz berechnet werden.
Die auf der Primärseite sichtbare Impedanz setzt sich (unter Vernachlässigung des Ohmschen Widerstandes der Primärwicklung) zusammen aus dem induktiven Blindwiderstand der primärseitigen Wicklung und der vom Sekundärkreis in den Primärkreis hinein transformierten Impedanz (diese kann den induktiven Blindwiderstand der Primärwicklung ganz oder teilweise aufheben). Die auf der Primärseite sichtbare Impedanz ergibt sich damit im Falle eines Transformators mit näherungsweise vollständiger magnetischer Kopplung zu [5]
mit der sekundärseitigen Impedanz Z (Lautsprecherimpedanz) aus Gleichung (4), der Induktivität L1 der primärseitigen Transformatorwicklung und der Induktivität L2 der sekundärseitigen Wicklung. Zur beispielsweisen Berechnung der primärseitig sichtbaren Impedanz gehen wir von einem NF-Übertrager mit L1=10H und L2=10mH, entsprechend einem Übersetzungsverhältnis für Widerstände von 1000:1, aus. Für den Betrag |Zp| der primärseitig sichtbaren Impedanz ergibt sich damit folgendes Diagramm:

Es ist prinzipiell der Verlauf der Lautsprecherimpedanz wieder zu erkennen. Wie erwartet sinkt die
primärseitig sichtbare Impedanz zu niedrigen Frequenzen (f<100Hz) deutlich ab. Die Ursache hierfür liegt direkt im Verhalten des Transformators für niedrige Frequenzen wie aus den allgemeinen Transformatorformeln hervorgeht. (Für Gleichströme- und Spannungen verschwindet natürlich die primärseitig sichtbare Impedanz bis auf den Ohmschen Widerstand der Primärwicklung vollständig.) Betrachtet man die primärseitig sichtbare Impedanz nach Ohmschem- und Blindanteil getrennt, so ergibt sich das unten stehende Diagramm.

Referenzen:
[1] de.wikipedia.org/wiki/Lorentzkraft
[2] de.wikipedia.org/wiki/Harmonischer_Oszillator
[3] en.wikipedia.org/wiki/Faraday's_law_of_induction
[4] en.wikipedia.org/wiki/Thiele/Small_parameters
[5] www radiomuseum.org/forum/die_allgemeinen_transformatorformeln2.html
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Die Frequenzabhängigkeit der Lautsprecherimpedanz

Hallo Herr Bauer,
vielen Dank für die anspruchsvolle Arbeit.
Mir ist nicht ganz klar, wie die Umgebung ( Luft ) in das rechenmodell eingeht.
Man weiß, dass Lautsprecher ohne Gehäuse, ( Box, Schallwand ) ggf. rasch zerstört werden.
Möglicher Weise ist die ausgeprägte Resonanz dafür eine Erklärung.
Ich habe ein Datenblatt eines Lautsprechers mit Messprotokoll, darin ist in der Übertragungsfunktion so
eine ausgeprägte Resonanz nicht zu erkennen. Wenn ich den Aufbau richtig verstanden habe, wurde der Lautsprecher in einer schalltoten Kabine gemessen, auf einer praktisch unendlich grossen Schallwand, so dass der Lautsprecher maximal gedämpft wird.
Was meinen Sie ?
Gruß aus dem Remstal
Georg Beckmann
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Die Frequenzabhängigkeit der Lautsprecherimpedanz

Hallo Herr Beckmann
Vielen Dank für ihr Interesse!
Die den Lautsprecher umgebende Luft geht in die Parameter r und s aus Gl. (1) ein.
Der Parameter r ist der mechanische Verlustwiderstand des Lautsprechers. Dieser setzt sich zusammen aus den Reibungsverlusten im Lautsprecher bei der Bewegung der Membran, aus der "Reibung" der Membran in der Umgebungsluft, aus der Erwärmung der Umgebungsluft durch die Kompression in einem geschlossenen Lautsprechergehäuse und aus dem (gewollten) Energieverlust durch Abstrahlung von Schallwellen ins "unendliche" bzw. gegen die Wand einer echofreien Kammer.
Der Parameter s ist die Federkonstante des Lautsprechers aus der sich die Rückstellkraft bei einer gegebenen Auslenkung der Membran ergibt. Die Rückstellkraft auf die Membran ergibt sich einerseits aus der elastischen Eigenschaft der Membran und andererseits aus der Kompression der Luft in einem geschlossenen Lautsprechergehäuse, ähnlich einer Gasdruckfeder.
Ein Lautsprecher ohne geschlossenes Gehäuse mit "Kompressionsbremse" wird natürlich bei gegebener Antriebskraft deutlich weitere Auslenkungen der Membran erfahren, was zu deren Beschädigung führen kann.
So weit ich das zitierte Datenblatt gelesen habe ist dort nicht die Impedanz als Funktion der Frequenz sondern der Schalldruck als Funktion der Frequenz angegeben. Das sind zwei völlig verschiedene Größen, insofern sind sich auch die Kurven natürlich nicht mal ähnlich.
Die eigentliche Herausforderung wenn es an die Bestimmung des Schalldrucks bzw. des
Wirkungsgrades eines Lautsprechers als Funktion der Frequenz geht ist die Ermittlung der
Zusammensetzung der Parameter r und s aus den Eigenschaften der Membran und den Eigenschaften des Gehäuses mit dem darin enthaltenen Luftvolumen. In dem konkreten Beispiel im obigen Artikel wurden für die Parameter r und s Näherungsweise die entsprechenden Eigenschaften der Membran (Thiele-Small Parameter Rms und 1/Cms) eines generischen Lautsprechers verwendet.
Gruß Jochen Bauer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Die elektrische Ersatzschaltung des Lautsprechers

Wir wie im Artikel #1 gesehen haben wird die Impedanz Z des Lautsprechers mit
für eine gegebene Frequenz ω signifikant von den mechanischen Eigenschaften des Lautsprechers
und der mechanisch-elektrischen Rückwirkung bestimmt.
Es stellt sich nun die Frage, ob es möglich ist eine rein elektrische Ersatzschaltung aus Widerständen, Kondensatoren und Induktivitäten zu bilden die den selben Impedanzverlauf über der Frequenz ω aufweist wie ein physikalisch vorhandener Lautsprecher.
Die Gründe für dieses Unterfangen sind:
- Eine, wenn auch ggf. komplizierte Anordnung von R, C und L Bauteilen ist für den Praktiker oft besser verständlich und greifbar als eine mathematische Formel Z(ω) für den Impedanzverlauf
über der Frequenz. - Eine Ersatzschaltung aus R, C und L Bauteilen kann ohne Anpassungen in einer Software zur Schaltungssimulation verwendet werden.
- In der Praxis können Endstufen bei voller Leistung ohne Geräuschentwicklung getestet werden.
Gehen wir von der Lautsprecherimpedanz Z aus Gl. (4) aus so ist zu sehen, dass sich diese in einen rein elektrischen Teil R + jωL und einem mechanisch-elektrischen Teil ZM gemäß
mit
aufspalten lässt. Der mechanisch-elektrische Teil ZM kann nach einigen Umformungen als
geschrieben werden. Diese Impedanz entspricht der Impedanz eines RLC Parallelkreises mit den Entsprechungen [1]
Offensichtlich lässt sich das mechanische Lautsprechersystem was die elektrische Impedanz angeht durch einen RLC Parallelkreis mit den Bauteilen RM, CM und LM ersetzen, wobei die Werte dieser Bauteile durch das Produkt Bl und die weiteren Parameter m,r und s des Lautsprechers gegeben sind.
Zu der Impedanz des mechanische Lautsprechersystems kommt nun, wie bereits beschreiben, der Gleichstromwiderstand R der Lautsprecherspule und deren Induktivität L additiv d.h. in Serie hinzu
und wir gelangen damit zu folgender Ersatzschaltung:

Wie erwartet, ergibt sich die Resonanzfrequenz des RLC Parallelkreises zu
Der Gütefaktor QM des mechanischen Lautsprechersystems (als harmonischer Oszillator betrachtet) entspricht der Güte des RLC Parallelkreises der Ersatzschaltung und ergibt sich damit zu [1]
An dieser Stelle ist noch eine Ergänzung angebracht, auf die mich Herr Prof. Rudolph aufmerksam machte:
Man kann den Einfluss der sich bewegenden Spule und die damit verbundene mechanisch-elektrische
Rückwirkung auch sehr schön experimentell sehen. Dazu kann man in einem alten, nicht mehr
benötigten Lautsprecher Membran und Spule durch festkleben fixieren (der Lautsprecher wird dadurch
aber natürlich für alle anderen Zwecke unbrauchbar). Bei still stehender Spule fällt nun die
mechanisch-elektrische Rückwirkung und damit die Resonanz-Überhöhung weg und die verbleibende
Impedanz ist Z=R+jωL. Der Betrag dieser verbleibenden Impedanz ist zum Vergleich im folgenden Diagramm dargestellt.

Im Falle einer vollständig fixierten Spule wird die elektrische Ersatzschaltung natürlich auf R und L in Serie reduziert, der Parallelresonanzkreis entfällt bzw. wird kurz geschlossen.
Eine weniger destruktive Methode um diese Zusammenhänge experimentell zu untersuchen ist die Verwendung eines elektro-dynamischen Lautsprechers. Bei diesem wird das Magnetfeld in dem sich die Spule bewegt nicht durch einen Permanentmagneten sondern durch einen Elektromagneten erzeugt. In diesem Fall kommt die mechanisch-elektrische Rückwirkung natürlich nur dann zustande wenn der Elektromagnet mit Strom versorgt wird.
Referenzen:
[1] Normierte Resonanzkurven von Schwingkreisen
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.