Allgemeingültige, lin. Theorie z. Dim. v. NF-Endstufen
Allgemeingültige, lin. Theorie z. Dim. v. NF-Endstufen
Allgemeingültige, linearisierte Theorie zur Dimensionierung von Niederfrequenz-Endstufen
aufgestellt: Michael Hentschel, Dipl.-Ing.
2720 Rotenburg (Wümme), im Mai 1981
1. Einleitung
Die Endstufen in Niederfrequenz-Endverstärkern haben die Aufgabe, eine große Ausgangsleistung zur Verfügung zu stellen. Die Dimensionierung muß in der Weise erfolgen, daß sich aus einem vorgegebenen Bauelement eine möglichst große, wenig verzerrte Ausgangsleistung mit optimalem Wirkungsgrad ergibt. Zur Anwendung können Röhren oder Transistoren kommen. Obwohl diese Bauelemente unterschiedliche Kennlinienfelder aufweisen, läßt sich hierfür jedoch eine allgemeingültige, linearisierte Theorie aufstellen. Es wird hierbei vom Ausgangskennlinienfeld des Bauelementes ausgegangen. Die Gemeinsamkeit beider Kennlinientypen ist, daß immer eine nicht aussteuerbare Restspannung UR vorhanden ist, siehe Bild 1.
Im nachfolgenden Aufsatz werden Endstufen mit Röhren und Transistoren betrachtet, wobei es für die Berechnung grundsätzlich keinen qualitativen Unterschied macht, ob es sich um Pentoden, Tetroden oder Trioden oder Transistoren handelt. Da heute bei Röhrenverstärkern jedoch vorwiegend Pentoden für diese Aufgabe herangezogen werden, wollen wir uns hinsichtlich der Ausgangskennlinienfelder auf die der Pentoden beschränken.

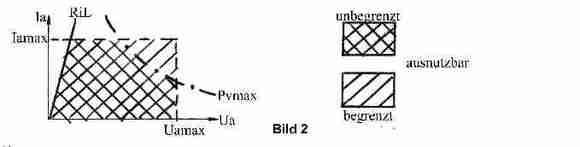
Weitere Einschränkungen des ausnutzbaren Kennlinienbereiches sind durch Verlusthyperbel, Spitzenstrom und die maximal zulässige Betriebsspannung gegeben. Hierfür ist der exakte Kennlinienverlauf zunächst einmal unerheblich. Somit ergibt sich im Ausgangskennlinienfeld des gegebenen Bauelementes ein aussteuerbarer Bereich, wobei hier zwischen dem unbegrenzt und dem begrenzt ausnutzbaren Bereich im Kennlinienfeld zu unterscheiden ist, siehe Bild 2.
2. Eintakt-A Endstufen (Single ended Class A)
Mit NF-Endstufen werden gewohnter Weise Musik und / oder Sprache übertragen, wo durchaus Pausen vorkommen, in denen keine Aussteuerung der Endstufe erfolgt. Hierfür ist es erforderlich, den Arbeitspunkt so zu legen, daß auch bei fehlender Wechselspannungsansteuerung eine Überbelastung des ausgewählten Bauelementes vermieden wird. Daraus folgt konsequenterweise, daß der zu wählende Arbeitspunkt sich im unbegrenzt ausnutzbaren Bereich befinden muß. Um darüber hinaus keine übermäßigen Verzerrungen zu bekommen, ist der Arbeitspunkt weiterhin so zu legen, daß eine möglichst große, möglichst symmetrische Aussteuerung des Bauelementes gegeben ist.
2.1 Endstufen mit Widerstandslast
Im allereinfachsten Fall ist der Lastwiderstand RL direkt an das verstärkende Bauelement gekoppelt, siehe Bild 3.

Somit erhält man im Ausgangskennlinienfeld gemäß Bild 4 direkt die entsprechende Arbeitskennlinie.

Bei sinusförmiger Ansteuerung erhält man:
ia = IA + îa * cos wt
und
ua = UA – ûa * cos wt
Hierbei wird aus der Stromversorgung die Leistung PSV = USV * IA entnommen. Die dabei zwangsläufig auftretende Verlustleistung PV verbleibt in Form von Wärme im verstärkenden Bauelement.
PV = 1 : T * ∫ [0 bis T] ua * ia * dt
PV = ½ *p * ∫ [0 bis 2p] (UA – ûa *cos wt) * (IA + îa * cos wt) * dwt
PV = UA * IA – ½ * ûa * îa
Am Lastwiderstand RL ergibt sich somit die Leistung PL zu:
PL = 1 : T ∫ [0 bis T] (USV – ua) * ia * dt
PL = ½ *p * ∫ [0 bis 2p] (USV - UA + ûa * cos wt) * (IA + îa * cos wt) * dwt
PL = (USV -UA) * IA + ½ * ûa * îa = PvL + Pa
PL = PvL + Pa
Die Leistung PL am Lastwiderstand setzt sich also zusammen aus einem Gleichstromanteil PvL, und der abgegebenen Wechselstromleistung Pa. Als Wirkungsgrad h bezeichnet man das Verhältnis von in Wechselstromleistung Pa zur gesamt eingesetzten Gleichstromleistung.
h = Pa : PSV = Pa : (Pv + PL) = Pa : (Pv + PL + Pa)
Hieraus ist leicht zu erkennen, daß man den Wirkungsgrad h erhöhen kann, wenn es einem gelingt, den Gleichstromanteil PvL gegen Null gehen zu lassen. Die Möglichkeit hierfür bietet sich durch eine induktive Lastankopplung des Lastwiderstandes RL mittels Übertrager an.
2.2 NF-Endstufen mit induktiver Lastankopplung durch Übertrager
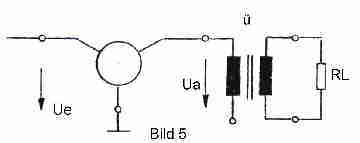
Die sich hierfür ergebende Schaltung ist die in Bild 5. Man beachte die Änderung gegenüber Bild 3.
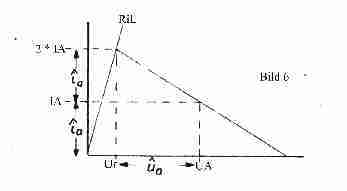
Im Ausgangskennlinienfeld ergibt sich wieder die Arbeitskennlinie gemäß Bild 6, wobei hier jetzt jedoch für Ra der durch den Übertrager übersetzte Lastwiderstand RL mit Ra = ü2 * RL anzusetzen ist.
Im Regelfall ist in der Praxis der Wert für USV vorgegeben. Demnach ist der Arbeitswiderstand Ra so festzulegen, daß die Ausgangsleistung Pa ein Maximum erreicht. Für eine idealisierte Theorie wird in den nachfolgenden Betrachtungen der Ausgangsübertrager als verlustlos angenommen, und die Kupferwiderstände der Wicklungen vernachlässigt. Somit kann die Ruhespannung im Arbeitspunkt mit UA = USV angenommen werden. Hiervon wird in den nachfolgenden Betrachtungen ausgegangen.
Die Ausgangsleistung Pa sei:
Gl. (1) Pa = ½ ûa * îa
Bei voller Stromausnutzung, und wegen der Forderung nach symmetrischer Aussteuerung ist:
îa = IA
und somit:
Gl. (2) ûa = îa * Ra = IA * Ra
Mit der festen Vorgabe UA = USV soll nun für ûa ein Ausdruck durch UA angegeben werden. Im Bild 6 kann man hierzu den folgenden Ausdruck entnehmen:
Gl. (3) ûa = UA - UR
Per Konvention wird die linke Grenzkennlinie des aussteuerbaren Kennlinienfeldteiles durch den Widerstand RiL gekennzeichnet. Damit ist UR festgelegt zu:
Gl (4) UR = 2 * IA * RiL
Gl. (4a) => RiL = UR : (2 * IA)
Setzt man nun Gleichung (4) in Gl. (3) ein so erhält man:
ûa = UA – 2 * IA * RiL
Durch gleichsetzen mit Gl. (2) erhält man:
IA * Ra = UA – 2 * IA * RiL
Hieraus ergibt sich für IA:
IA = UA : (Ra + 2 * RiL)
Unter Anwendung von Gl. (1) ergibt sich die Ausgangsleistung Pa zu:
Pa = ½ * IA * Ra * IA
Pa = ½ * IA2 * Ra
Durch Substitution von IA mit UA : (Ra + 2*RiL) ergibt sich
Gl. (5) Pa = ½ * (UA2 * Ra) : (Ra + 2 * RiL)2
Mit dPa/dRa = 0 erreicht die Ausgangsleistung Pa ihr Maximum Pamax. Dieser Punkt wird erzielt bei:
Gl. (6) Ra = 2 * RiL
Für diese Bedingung wird die Ausgangsleistung Pa zu:
Pa = Pamax = UA2 : 16 * RiL
Mit IA = UA : (Ra + 2*RiL) = UA : 4 * RiL
folgt hieraus, daß der Arbeitspunkt auf der Nullpunktgeraden 4 * RiL liegen muß.
Der Wirkungsgrad h ergibt sich hieraus zu:
h= Pa : PSV = (UA2 * 4 * RiL) : (UA2 * 16 * RiL) = 0,25
Diese Dimensionierung ist jedoch nur solange gültig, bis die 4RiL-Gerade in einem Punkt die Grenzhyperbel für die maximale Verlustleistung Pvmax des Bauelementes schneidet. Es ergibt sich ein Grenzwert für die Ruhespannung UAGrenz aus:
UAGrenz = IA * 4 * RiL und
UAGrenz = Pvmax : Ia zu
Gl. (7) UAGrenz = ÖPvmax * 4 * RiL
Wird dieser Grenzwert jedoch überschritten, das bedeutet: UA > UAGrenz, was im Regelfall bei modernen Bauelementen ohne Probleme möglich ist, so muß ein anderer Ansatz für die Dimensionierung für Ra gemacht werden. Auf Grund der Möglichkeit, daß in Pausen die Aussteuerung gegen Null gehen kann, darf der zu wählende Arbeitspunkt im äußersten Fall auf der Verlusthyperbel liegen. Die größtmögliche Ausgangsleistung Pa wird erreicht, wenn ûa und îa maximale Werte annehmen. Auf Grund der Forderung nach maximaler, symmetrischer Stromaussteuerung ist îa = IA zu wählen, und da îa möglichst groß sein soll, ist IA - bei vorgegebenen Ua - auf den höchstmöglichen Wert, das bedeutet auf die Verlusthyperbel zu legen.
Daraus folgt: Gl. (8) IA = Pvmax : UA
Entsprechend ist die Bedingung für die Dimensionierung des Arbeitswiderstandes Ra:
Ra = ûa : îa = ûa : IA
Gemäß Gl. (3) ist der höchste Wert den ûa annehmen kann:
ûa = UA - UR = UA - 2* RiL * IA
Für den so zu wählenden Arbeitswiderstand Ra ergibt sich hiermit die neue Dimensionierungsvorschrift zu:
Ra = (UA – 2 * RiL * IA) : IA = (UA : Ia) – 2 * RiL
Daraus folgt:
Gl. (9) Ra = (UA2 : Pvmax) – 2 * RiL
Aus den Grenzwerten RiL und Pvmax des vorgesehenen Verstärkerelementes, und der vorgegebenen Betriebsspannung aus der Stromversorgung USV = UA, ist somit der Arbeitswiderstand festgelegt. Setzt man jetzt die Gl. (9) in Gl. (5) ein, errechnet sich die Ausgangsleistung Pa, die bei Vollaussteuerung erreichbar ist, zu:
Pa = (UA2 : 2) * (UA2 : Pvmax – 2 * RiL) : (UA2 : Pvmax)
Gl. (10) Pa = Pvmax : 2 – (Pvmax2 : UA2) * RiL
Der Wirkungsgrad h ergibt sich unter diesen Gegebenheiten zu:
h = Pa : PSV = Pa : Pvmax
h = (Pvmax : 2 – (Pvmax2 : UA2) * RiL) : Pvmax
Gl. (11) h = ½ - (Pvmax : UA2) * RiL
Unter Einbeziehung von Gl. (9) folgt somit letztendlich:
Gl. (11a) h =½ – RiL : (Ra + 2RiL) = Ra : (2 * (Ra + 2 * RiL))
Der Wirkungsgrad h kann rein theoretisch entsprechend Gl. (11) bis zum Grenzwert hmax = ½ ansteigen, wenn RiL gegen Null (RiL = 0) geht oder alternativ UA immer größere Werte annimmt. Praktisch ist dem dadurch eine Grenze gesetzt, daß die maximale Ausgangsspannung Uamax nicht überschritten werden darf, wenn es nicht zu einem Durchbruch im Verstärkerelement kommen soll.
Es muß also stets gewährleistet sein, daß UA + ûa ≤ Uamax bleibt. Für kleine Werte von RiL kann vereinfacht gesetzt werden UA ≤ Uamax : 2
Exakter gilt jedoch:
Gl. (12) UAmax = Uamax : 4 + √(Uamax2 :16 + (RiL * Pvmax))
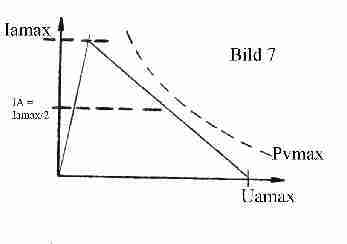
Sofern schaltungstechnisch noch eine zusätzliche Spitzenstrombegrenzung vorliegt, ergibt sich entsprechend Bild 6, daß: 2 * îa = 2 * IA ≤ Iamax bleiben muß. Aus Bild 7 folgt gezwungenermaßen für den erforderlichen optimalen Arbeitswiderstand Ra:
Gl. (13) Ra = (Uamax – Iamax * RiL) : Iamax = Uamax : Iamax – RiL
und zwar unter der Bedingung, daß der Arbeitspunkt IA = Iamax : 2 stets unter der Verlusthyperbel Pvmax. liegt.
In der nachfolgenden Tabelle 1 sind die sich ergebenden Dimensionierungsrichtlinien für alle in Frage kommenden Möglichkeiten erschöpfend dargestellt. Für den Fall, daß neben RiL und Pvmax auch Uamax und Iamax als Grenzen auftreten, ergeben sich zwei mögliche Arbeitspunkte. Hierbei ergibt der Betrieb mit dem größeren Arbeitswiderstand Ra auch den größeren Wirkungsgrad h, und damit auch die größere Ausgangsleistung Pa, weil auch in beiden Betriebsfällen aus der Stromversorgung die Leistung Pvmax aufgenommen wird.
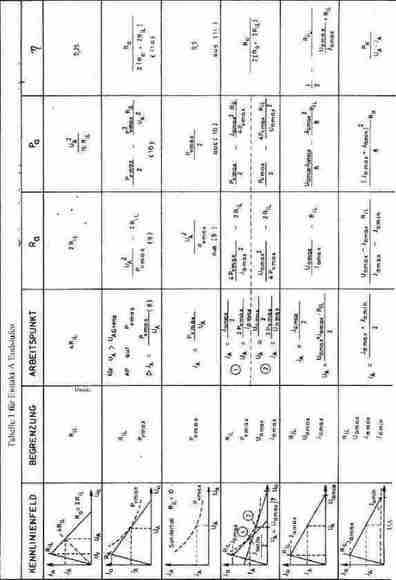
3. Gegentakt NF-Endstufen mit induktiver Lastankopplung
3.1. Gegentakt-A Endstufen (Class A Push-Pull)
Eine eingehendere rechnerische Betrachtung für den Gegentakt-A Betrieb soll an dieser Stelle nicht unternommen werden, da derartige Endstufen gegenüber dem Eintakt-A Betrieb keinen echten Vorteil bieten und von der Konzeption her eher die Ausnahme bilden, so daß wir direkt zum Gegentakt-B Verstärker übergehen werden.
3.2. Gegentakt-B Endstufen (Class B Push-Pull)
Diese Betriebsart hat gegenüber dem Eintakt-A und Gegentakt-A Betrieb den Nachteil, das sich durch die nichtlinearen Kennlinien der Bauelemente auch im linearisierten Bereich der gegeneinander aufgetragenen Kennlinien noch deutliche Übernahmeverzerrungen ausbilden, weil einfach die gegenseitige Auskompensierung fehlt. Und die erweisen sich für Klangübertragung als durchaus störend. Damit liegt die Gegentakt-B Endstufe nicht so günstig wie die Gegentakt-A Endstufe. Lediglich in der unmittelbaren Umgebung des Arbeitspunktes findet eine teilweise Linearisierung statt. Aus diesem Grund haben sich heute auch überwiegend die sogenannten Gegentakt-AB Verstärker (Class A/B Push-Pull) durchgesetzt, die von der Arbeitspunktauslegung, und vom Arbeitsverhalten, her so etwas wie ein Mittelding zwischen Eintakt-A/Gegentakt-A und Gegentakt-B Verstärkern sind. Bei kleinen Signalansteuerungen arbeiten sie im Gegentakt-A Betrieb, um dann bei höheren Ansteuerpegeln zum Gegentakt-B Betrieb überzugehen, was sich in einer ansteuerungsabhängigen Verschiebung des Arbeitspunktes äußert. Indes ist hierfür zu erwähnen, daß deren rein rechnerische Betrachtung äußerst aufwendig und kompliziert ist, da u.U. mit den unterschiedlichen Ansteuerungen aus den Kennlinienfeldern mit den einzelnen Kennlinienabschnitten zuerst die Beträge für die Verzerrungen bzw. Klirrfaktoren (k2, k3, k4, k5 etc.) und die daraus resultierenden Gleichstromkomponenten zu ermitteln sind, um damit dann die Arbeitspunktverschiebungen zu untersuchen, so daß auf Grund dieser Tatsache an dieser Stelle daher eine rechnerische Behandlung nicht unternommen werden soll. Für das Verständnis kann man sie jedoch, wie bereits erwähnt, als ein Mittelding zwischen Gegentakt-A und Gegentakt-B Verstärkern ansehen.
Die Gegentaktschaltung führt, wie bereits erwähnt, bekanntlich zu einer gewissen Linearisierung der Übertragungskennline der Verstärkerelemente. Wird auch im Gegentakt im A-Betrieb gearbeitet (es fließt während der ganzen Signalperiode Strom), so ergibt sich gegenüber den Eintaktbetrieb lediglich der Vorteil des Linearisierungseffektes, den man in modernen Endstufen durch Gegenkopplungsmaßnahmen mindestens ebensogut erzielen kann. Eine wesentliche Verbesserung gegenüber Eintakt-A und Gegentakt-A Betrieb ist bei der Gegentaktschaltung erst durch die Einstellung des Arbeitspunktes auf B-Betrieb möglich (d.h., der Arbeitspunkt liegt im unteren Bereich - Knickpunkt – der Arbeitskennlinie). Hierbei fließt in jedem Verstärkerelement nur während einer Halbwelle Strom, siehe Bild 8. Im Ausgangsübertrager werden die beiden Halbwellen wieder zusammengesetzt, und entsprechend dem Übersetzungsverhältnis an den Lastwiderstand abgegeben.

Der große Vorteil der B-Einstellung ist der, daß bei fehlender Ansteuerung durch die Verstärkerelemente
auch kein Strom fließt, und somit aus der Stromversorgung auch keine Leistung entnommen wird. Die Stromaufnahme ist demnach von der Aussteuerung abhängig, d.h., die Leistungsabgabe, und die der Stromversorgung entnommene Leistung, hängen direkt vom Aussteuerungsgrad ab. Gegenüber der Eintakt-Endstufe, bei der konstant und unabhängig von der Ansteuerung Strom fließt, und somit der Stromversorgung Leistung entzogen wird, ist dies ein wesentlicher, beachtlicher Vorteil.
Da eine Gegentakt-Endstufe symmetrisch aufgebaut ist, ist es ist ausreichend für die Dimensionierung der Endstufe nur das Ausgangskennlinienfeld eines Verstärkerelementes zu betrachten, beide Hälften sind als gleichwertig anzusehen, und für jede Halbwelle stellt das jeweils stromlose Verstärkerelement keine Belastung des Ausgangsübertragers dar. Der auf die Primärseite des Übertragers transformierte Lastwiderstand RL errechnet sich mit:
Raa = ü2 * RL
Da jedes Verstärkerelement an der halben Primärwicklung angeschlossen ist, und diese für den B-Betrieb Gleich- und Wechselstrommäßig parallel liegen, ergibt sich der wirksame Arbeitswiderstand Ra für den Gegentakt-B Betrieb zu:
(Anm.: Bei Gegentakt-A Betrieb sind die beiden Primärwicklungshälften wechselstrommäßig in Reihe geschaltet! Im B Betrieb stellt der Ausgangsübertrager primärseitig einen Spartrafo dar; bei fehlender, sekundärseitiger Last resultieren daraus primärseitig Spannungsüberhöhungen die zu Überschlägen führen können!)
Ra = Raa : 4 => Raa = 4 * Ra für B-Betrieb
4 * Ra = ü2 * RL Þ Ra = (ü2 * RL) : 4
Im Arbeitspunkt ist die Spannung Ua = USV unter Vernachlässigung der Kupferwiderstände der Primärwicklung des Übertragers. Die Aussteuerungsverhältnisse werden in Bild 9 hinreichend dargestellt.

Für die Betrachtung der Zusammenwirkung beider Verstärkerelemente sind im Bild 10 die beiden Ausgangskennlinienfelder gegeneinander aufgetragen.

Als Grundlage für unsere weiteren Betrachtungen wird Bild 9 herangezogen. Jedes Verstärkerelement erbringt die halbe Ausgangsleistung. Somit gilt:
Pa = Pa1 + Pa2 mit Pa1 = Pa2
Als Kennzeichnung der Aussteuerung wird der Aussteuergrad m mit 0 £ m £ 1 eingeführt. Wenn mit ûa und îa die Werte für Vollaussteuerung festgelegt werden, so erhält man:
ua f(wt) = UA – m * ûa * cos wt
ia f(wt) = m * îa * cos wt für -p:2 £ wt £ +p:2
ia f(wt) = 0 für p:2 < wt < 3 * p:2
Damit wird aus der Stromversorgung die folgende Leistung entzogen:
PSV = ½ * p ∫ [-p bis +p] UA * ia (wt) * dwt
PSV = ½ * p ∫ [-p:2 bis +p:2] UA *m *îa * cos wt * dwt
PSV = 1 : p * m * UA * îa
PSV = m * UA * IA
Als Verlustleistung verbleibt im Verstärkerelement:
Pv1 = ½ * p ∫ [-p bis +p] ua (wt) * ia (wt) * dwt
Pv1 = ½ * p ∫ [-p:2 bis +p:2] (UA - m *ua * cos wt) * m *ia * cos wt *dwt
Pv1 =m * UA * IA – m2 : 4 – ûa * îa
Im Arbeitswiderstand Ra wird somit die Leistung Pa1 umgesetzt:
Pa1 = ½ *p ∫ [-p:2 bis +p:2] m *ûa * cos wt * m *îa * cos wt *dwt
Pa1 = m2 : 4 – ûa * îa
Für die nicht aussteuerbare Restspannung Ur folgt gemäß Bild 9:
Gl. (1) Ur = UA – ûa = îa * RiL
mit ûa = îa * Ra folgt aus Gl. (1)
Gl. (2’) îa = (UA – Ur) : RiL
Gl. (2) îa = UA : (Ra + RiL)
Beziehungsweise unter Berücksichtigung des Aussteuergrades m für îa und ûa:
Gl. (2a) m * îa = m * UA : (Ra + RiL)
Gl. (3) m * ûa = m * UA * Ra : (Ra + RiL)
Die Gl. (2) und Gl. (3) ergeben für die Ausgangsleistung Pa1 unter Berücksichtigung des Aussteuergrades m:
Gl. (4) Pa1 = m2 * UA2 : 4 * Ra : (Ra + RiL)2
Der Gleichstrom IA ist aussteuerungsabhängig gemäß:
IA = ½ * p ∫ [0 bis 2p] m * îa * cos wt * dwt
Gl. (5) IA = m * îa : p = m : p * UA : (Ra + RiL)
Aus der Stromversorgung wird die folgende Leistung PSV gezogen:
Gl. (6) PSV1 = m : p * UA2 : (Ra + RiL)
Daraus folgt für den Wirkungsgrad h:
Gl. (7) h = Pa1 : PSV1 = m * p : 4 * Ra : (Ra + RiL)
Die Verlustleistung Pv1 ergibt sich mit Gl. (4) und Gl. (6) zu:
Pv1 = PSV1 – Pa1 = m : p * UA2 : (Ra + RiL) – m2 : 4 * UA2 * Ra : (Ra + RiL)2
Gl. (8) Pv1 = UA2 : (Ra + RiL) * (m : p – m2 : 4 * Ra : (Ra + RiL)
Die Verlustleistung Pv1 erreicht ihren Maximalwert in Abhängigkeit vom Aussteuerungsgrad m unter der Bedingung, daß:
d/dm * Pv1 = 0 = 1 : p - 2 * m : 4 * Ra : (Ra + RiL)
Daraus ergibt sich ab diesem Punkt ein kritischer Aussteuerungsgrad mkrit zu:
Gl. (9) mkrit = 2 * (Ra + RiL) : p * Ra
Im allgemeinen kann man Ra > RiL annehmen, damit wird mkrit < 1.
Für RiL = 0 ergibt sich mkrit = 2 : p = 0,66.
Mit dieser Betrachtung kann nun ein Dimensionierungshinweis für Gegentakt-B Endstufen angegeben werden. Die Verlustleistung Pvmax ist hierbei als zulässige Grenze anzusehen, hierfür ist sicherzustellen, daß die Verlustleistung Pv1 nicht Pvmax beim kritischen Aussteuerungsgrad mkrit übersteigt.
Setzen wir mit Pv1 = Pvmax den Grenzwert, so erhalten wir aus Gl. (8) die Lösung, wenn für m der Grenzwert mkrit eingesetzt wird:
Pvmax = Pv1 f (mkrit) = {UA2 * 2 * (Ra + RiL) : ((Ra + RiL) * p * Ra )} * {1 : p - (2 * Ra * (Ra + RiL)) : (4*p* Ra * (Ra + RiL))}
Gl. (10) Pvmax = UA2 : p2 * Ra
Da die Kennlinie für Pvmax nicht bis RiL, sondern maximal bis mkrit ausgesteuert werden kann, erscheint in Gl. (10) auch RiL nicht. Wenn Ua = USV und Pvmax vorgegeben sind, erhält man Ra mit:
Gl. (11) Ra = UA2 : p2 * Pvmax
Die Gleichungen (10) und (11) gelten jedoch nur solange, wie bei Vollaussteuerung die Durchbruchsspannung Uamax des Verstärkerelementes und / oder der Spitzenstrom Iamax nicht überschritten wird. Wenn RiL klein ist, gilt auch hier:
UA £ Uamax : 2
Gl. (12) UAmax = Uamax * (Ra + RiL) : (2 * (Ra + RiL : 2))
Liegt eine Strombegrenzung vor, so muß îa £ Iamax gehalten werden, aus
Gl. (2) îa = UA : (Ra + RiL) folgt mit der Grenze Îa = Iamax
Gl. (13) Ra = UA : Iamax - RiL
Im Bild 11 sind Ausgangsleistung Pa1, Verlustleistung Pv1, Stromversorgungsleistung PSV und der Wirkungsgrad h, in auf die maximale Verlustleistung Pvmax normierter Form über den Aussteuerungsgrad m aufgetragen. Hierfür ist der Arbeitswiderstand Ra/RiL = 1/r = 10 gewählt worden. Die erforderlichen Gleichungen erhält man durch Division der Gleichungen (4), (6), (8) und (7) mit Gl. (10).
Gl. (10) Pvmax = UA2 : p2 * Ra
Gl. (14) Pa1 : Pvmax = m² * p² : 4 * (Ra : (Ra + RiL))²
Pa1 : Pvmax = m² * p² : (4 * (1 + r)²) normiert!
Gl. (15) PSV1 : Pvmax = m * p * Ra : (Ra + RiL)
PSV1 : Pvmax = m * p : (1 + r) normiert!
Gl. (16) Pv1 : Pvmax = (p² * Ra : (Ra + RiL)) *( m : p - m² : 4 * Ra : (Ra + RiL))
Pv1 : Pvmax = p² : (1 + r) * (m : p - m² : (4 * (1 + r))) normiert!
Gl. (17) h = m * p : 4 *Ra : (Ra + RiL))
h = m * p : (4 * (1 + r)) normiert!
Gl. (9a) mkrit = 2 * (Ra + RiL) : (p * Ra)
mkrit = 2 : p* (1 + r) normiert!

Die wichtigsten Beziehungen für die Dimensionierung von Gegentakt-B Endstufen enthält die nachfolgende Tabelle 2
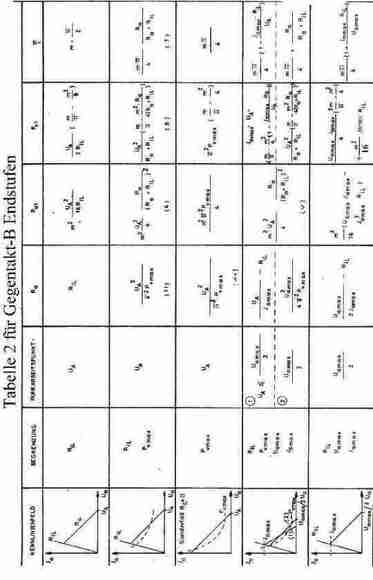
3.3 Komplementäre Transistor Endstufen
Die mit komplementären Transistorpaaren üblichen Grundschaltungen, wie sie heute verwendet werden, sind in den Bildern 12.1 und 12.2 dargestellt. Sie unterscheiden sich im wesentlichen nur durch die Treiberstufe.
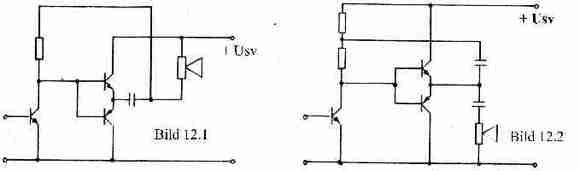
In der Grundschaltung 12.1 wird der Lastwiderstand RL – üblicherweise der Lautsprecher – vom Kollektorstrom des Treibertransistors durchflossen, während er hingegen in der Schaltung 12.2 stromlos bleibt. Insbesondere bei Endstufen höherer Ausgangsleistung, ist somit die Variante aus Bild 12.2 zu bevorzugen. Die bereits ermittelten Gleichungen aus Abschnitt 3.2 werden wiederum für eine Dimensionierung herangezogen. Dabei wird UA = USV : 2 und Ra = RL gesetzt.
Wir ermitteln also aus den Gleichungen:
3.2 - Gl. (4) Pa1 = m2 * USV2 : 16 * RL : (RL + RiL)2
(1)
3.2 - Gl. (5) IA = m : 2 * p * USV : (RL + RiL)
(2)
3.2 - Gl. (6) PSV = m : 4 * p * USV2 : (RL + RiL)
(3)
3.2 - Gl. (7) h = m * p : 4 * RL : (RL + RiL)
(4)
3.2 - Gl. (8) Pv1 = USV2 : 4 * (RL + RiL) * (m : p – m2 : 4 * RL : (RL + RiL)
(5)
3.2 - Gl. (9) mkrit = 2 * (RL + RiL) : p * RL
(6)
3.2 - Gl. (10) Pvmax = USV2 : 4 *p2 * RL
(7)
Mit Normierung auf die maximale Verlustleistung Pvmax ergeben sich die Gleichungen (14) bis (17) aus Kapitel 3.2. Hierfür wurde angesetzt:
Pvmax = USV2 : 4 *p2 * RL
sowie: RiL : RL = r
Für ein schnelle Abschätzung der erreichbaren Werte, kann vereinfacht mit RiL = 0 gerechnet werden. Hierbei wird die Sättigungsspannung der Transistoren gegenüber der Betriebsspannung aus der Stromversorgung vernachlässigt.
Pa1 = m2 * USV2 : 16 * RL
(1a)
IA = m : 2 * p * USV : RL
(2a)
PSV = m : 4 * p * USV2 : RL
(3a)
h = m * p : 4
(4a)
Pv1 = USV2 : 4 * RL * (m : p – m2 : 4)
(5a)
mkrit = 2 : p
(6a)
Pvmax = USV2 : 4 *p2 * RL
(7a)
Wenn bei m = 1 (d.h. Vollaussteuerung) die gesamte Ausgangsleistung der Endstufe mit Pa = Pa1 + Pa2 angegeben wird, so ergibt sich mit
Pa = USV2 : 8 * RL
(8)
die Näherungslösung:
Pvmax = USV2 : 4 *p2 * RL = 2 : p2 * Pa ≈ 0,2 * Pa
(9)
3.4 Dimensionierung der Transistortreiberstufe
Zur Sicherstellung der Vollausteuerung der Endstufentransistoren ist eine exakte Dimensionierung der Treiberstufe unumgänglich. Die zwei häufig benutzten Schaltungsvarianten sind in den Abbildungen 12.1 und 12.2 dargestellt. In der einschlägigen Literatur ist der Rechengang für die Dimensionierung von Treiberstufen hinreichend erklärt, wobei hier insbesondere das Transistorkompendium Teil III der Valvo GmbH zu empfehlen ist. Aus diesem Grund wird an dieser Stelle auch auf eine weitere, eingehende Betrachtung verzichtet
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Dimensionierung von Endstufen
Um Endstufen zu dimensionieren geht man von Arbeitskennlinien aus. Die klassische Methode dabei ist es, eine Kennlinienschaar der Röhre aufzunehmen (oder aus einem Datenblatt zu entnehmen) und mit der Zeichenmethode die Arbeitskennlinie bei gegebenen Lastwiderstand zu gewinnen.
Im Zuge meiner Experimente mit dem RoeTest habe ich mir Gedanken gemacht, welche alternativen Möglichkeiten es gibt, die Arbeitskennlinie zu ermitteln. Meine Gedanken habe ich auf meiner Internetseite in einer pdf-Datei niedergeschrieben:
Arbeitskennlinien (pdf)
Dabei bin ich zum Ergebnis gekommen, dass die einfachste und schnellste Möglichkeit ist, einfach entsprechende Lastwiderstände einzuschleifen und mit einer "realen" Schaltung eine Kennlinie aufzunehmen. Damit erspart man sich umfangreiche Berechnungen und Zeichnungen, sowie Zeit (vor allem wenn man die Möglichkeit hat, Kennlinien auf automatischem Wege aufzunehmen).
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.