Impedanz von Kondensatoren

Vor allem aufgrund ihrer Anschluß-Drähte, aber auch infolge der Bauform, verhalten sich Kondensatoren bei höheren Frequenzen nicht mehr rein kapazitiv, sondern zeigen Serien-Resonanz-Verhalten, ehe sie sich schließlich induktiv verhalten. Diese Eigenschaften zu kennen, ist wichtig, wenn Kondensatoren zum "Abblocken" verwendet werden sollen. 

Im 4. Band von "Günther, H.; Richter, H.: Schule des Funktechnikers, Sondergebiete, 7.A., Frankh, 1951" werden hierzu Beispiele gezeigt.

Frequenz-Verhalten von Kondensatoren

Bei Kondensatoren interessiert hauptsächlich deren Eigeninduktivität im Bereich sehr hoher Frequenzen. Da ein Kondensator im allgemeinen hochfrequente Spannungen kurzschließen muß, ist seine "Eigeninduktivität" von großer Bedeutung; sie kann unter Umständen die Wirksamkeit des ganzen kapazitiven Kurzschlusses in Frage stellen.

Solange dem Kondensator Frequenzen zugeführt werden, die unterhalb seiner Eigenfrequenz liegen, verhält er sich wie ein kapazitiver Widerstand 1/ωC. Infolge der Induktivität der Zuleitungen und der eigentlichen Kondensatorbelege tritt jedoch bei einer bestimmten Frequenz Serienresonanz auf. Oberhalb dieser Frequenz verhält sich dann der Kondensator genau so wie eine Induktivität, ist also nicht mehr als kapazitiver Kurzschluß verwendbar.

Ein gutes Bild über die Größenordnungen, bei denen die "Eigenresonanz der Kondensatoren“ liegt, vermitteln Messungen von Opitz und Klemt, von denen hier einige gezeigt werden sollen.

Zunächst sehen wir in Abb. 1988 einige Kurven, die das Spannungsverhältnis U1/U an Glimmer-Wickel-kondensatoren in Abhängigkeit von der Frequenz f zeigen. U ist dabei die angelegte Meßspannung, U₁ die am Kondensator auftretende Spannung. Man hat sie sich an der Serienschaltung der Kondensator-Kapazität und der Kondensator-Induktivität liegend zu denken. Bei Auftreten von Serienresonanz wird diese Spannung natürlich Null bzw. bei Kondensatoren mit Verlusten erreicht sie einen Kleinstwert. Demnach wird auch der Wert U₁/U bei Auftreten der Serienresonanz Null.

Wie man aus den Kurven sieht, tritt die Serienresonanz bei um so kleineren Frequenzen auf, je größer die Nennkapazität des Kondensators ist. Das ist verständlich, weil ja mit wachsender Kapazität größere Belege vorhanden sind, die eine entsprechend größere Selbstinduktion haben, so daß die Resonanzfrequenz entsprechend tief liegt. Die Kurven zeigen, daß bei dieser Art von Kondensatoren schon bei verhältnismäßig niederen Frequenzen mit Serienresonanz gerechnet werden muß. Man sieht also, daß man auch bei der Verwendung guter Kondensatoren bei größeren Frequenzen nicht immer ohne weiteres an kapazitive Kurzschlüsse glauben darf.

 

Abb. 1989 zeigt die Spannungskurven gleichartiger Kondensatoren, jedoch mit einer 2,5 cm langen Gesamtzuleitung. Man erkennt, deutlich den Einfluß. der Induktivität dieser Zuleitung. Vergleicht man z. B. die Kondensatoren von 400 pF in Abb. 1988 und Abbild 1989, so sieht man, daß im ersten Fall die Serienresonanz erst bei etwa 70 MHz, im zweiten Fall dagegen schon bei etwa 48 MHz auftritt. Schuld daran sind allein die Zuleitungen, die den Kondensator in einem Frequenzgebiet unbrauchbar machen, das bei Vermeidung der Leitungen noch erfaßt werden könnte.

 

Schließlich zeigen wir noch in Abb. 1990 entsprechende Kurven für Röhrchenkondensatoren, die eine Gesamtzuleitung von etwa 1,8 cm Länge besitzen. Die Werte liegen hier durchweg etwas günstiger als bei den anderen Kondensatoren.

Trotz der an sich hervorragenden Ausführung der modernen Kondensatoren erkennt man, daß sie bereits verhältnismäßig früh in Serienresonanz geraten und deshalb bei sehr hohen Frequenzen mit Vorsicht zu verwenden sind.

Man wird sich stets überlegen, welche Kleinstkapazität 1/ωC in der betreffenden Schaltung für einen kapazitiven Kurzschluß gerade noch zulässig ist und wird diesen Wert dann einbauen.

Dadurch vermeidet man unnötig tiefe Serienresonanzen durch unnötig große Kapazitäten. Sind sehr große Kondensatoren erforderlich, weil beispielsweise gleichzeitig noch eine Frequenz kleineren Wertes kurzgeschlossen werden soll, so kann man sich durch Parallelschaltung dieser großen mit einer kleinen, aber annähernd selbstinduktionsfreien Kapazität helfen.

Bei ganz besonders großen Kapazitäten ist jedoch auch mit den besten und kleinsten Kondensatoren nichts mehr anzufangen, so daß man dazu übergehen muß, als den einen Kondensatorbelag z. B. das Chassis des Gerätes und als anderen Belag eine Metallplatte zu verwenden, auf die das zu überbrückende Schaltelement direkt montiert ist. Unter Zwischenlage einer dünnen Schicht Glimmer oder Trolitul kann man dann die Platte unmittelbar mit dem Schaltelement auf das Chassisblech schrauben. Dieses Verfahren liefert einen wirklich guten kapazitiven Kurzschluß selbst noch im Dezimeterwellengebiet und muß unbedingt angewendet werden, weil andere Mittel restlos versagen.

Nachtrag aus: "Vilbig, F.; Zenneck, J.: Fortschritte der Hochfrequenztechnik Bd. 3, VAG, 1954"

Wie man hieraus erkennen kann, ist beim Ersatz defekter Kondensatoren sowohl auf deren Bauform, als auch auf die (maximale) Länge der Anschlußdrähte zu achten.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Von meinem Freund Hans Knoll stammt das Buch "Thiesbürger, K.H.: Der Elektrolyt-Kondensator, 3.A., FRAKO, 1982". Auf 220 Seiten wird darin die Technologie der Elektrolyt-Kondensatoren beschrieben.

Elektrolyt-Kondensatoren sind aufgrund des Elektrolyten und der damit verbundenen Chemie in ihren Eigenschaften sehr viel komplexer und komplizierter als Wickel-Kondensatoren oder keramische Kondensatoren.

Dies hier ist ein Ausschnitt aus Kapitel III.9 "Temperatur- und Frequenzabhängigkeit einiger Parameter".

III.9.1 Temperatur- und Frequenzabhängigkeit des Scheinwiderstandes Z

Der (qualitative) Verlauf Z(δ) und Z(f) läßt sich aus einer Ersatzschaltung gemäß Abb. 29 ableiten.

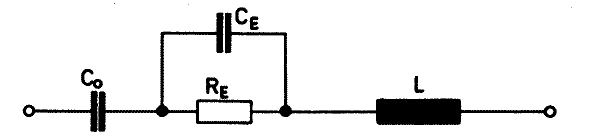Abb. 29

 

Dabei ist:

• C₀ die durch die Oxydschicht(en) gegebene Kapazität,
• R_E die Summe aller Zuleitungsverluste, also insbesondere der ohmsche Widerstand des Elektrolyt-Papier-Gemisches,
• L Die durch die "Geometrie" der (inneren) Zuleitungen zum Wickel verursachte Induktivität und die (dagegen vernachlässigbare) Induktivität des Wickels selbst,
• C_E die statische aus Anoden- und Katodenfolie gebildete Kapazität, die in erster Näherung bei praktisch üblichen Konstruktionen mindestens zwei Zehnerpotenzen kleiner ist als die Oxydschicht-Kapazität C₀.

Für den Scheinwiderstand Z (den Betrag des komplexen Wechselstromwiderstandes) ergibt sich mit diesen Definitionen und Annahmen eine Frequenzabhängigkeit Z (f), wie sie ideallisiert in Abb. 30 dargestellt ist:

Z fällt zunächst mit steigender Frequenz, bleibt dann in einem größeren Frequenzbereich mehr oder weniger konstant und steigt (nach Durchlaufen eines Resonanzminimums) bei hohen Frequenzen mit dieser wieder an.

Zum besseren Verständnis eines solchen Frequenzverhaltens seien die drei Bereiche niedriger, mittlerer und hoher Frequenzen getrennt betrachtet, was dadurch erleichtert wird, daß sich der Wert der Induktivität L sehr gut eingrenzen läßt:
Die erwähnte "Geometrie" der Wickelzuleitungen betrifft in erster Linie den Abstand (in Follenlängsrichtung) zwischen den beiden Kontaktfahnen zur Anoden- und Katodenfolie innerhalb des Wickels und die Art der "Leitungsführung" zu den äußeren Anschlußelementen. Im Rahmen sinnvoller praktischer Möglichkeiten sind nun Qualitäts-Kondensatoren der verschiedensten Größe und Spannung unter diesen Gesichtspunkten sehr ähnlich aufgebaut, so daß L (von Sonderkonstruktionen abgesehen) fast eine Konstante des Elektrolyt-Kondensators (in Wickeltechnik) darstellt und praxisnah mit

L ≈ 20 ● 10^-9 H = 20 nH

angenommen werden kann. (Das entspricht bei 10⁶ Hz einem induktiven Widerstand von ωL ≈ 0,13 Ω).

Die in diesem Wert enthaltene reine Wickelinduktivität liegt dagegen bei sorgfältigem Aufbau in der Größenordnung 10^-13 H = 10^-4 nH und ist damit hier völlig bedeutungslos!

1. niedrige Frequenzen (Größenordnung 10² Hz)
   R_E und erst recht der induktive Widerstand R_L = ωL sind vernachlässigbar klein.
   Wesentlich wirksam ist deshalb nur die Kapazität C₀, so daß hier
   Z ≈ Z₁ = 1/ωC₀
   ist. In einem doppelt-logarithmischen System (Abb. 30) mit gleichem Koordinatenmaßstab ist Z, eine "unter 45⁰ fallende" Gerade.
2. mittlere Frequenzen (Größenordnung 10⁴ Hz)
   Z₁ ist hier so klein (geworden), daß überwiegend der (ohmsche) Widerstand R_E wirksam wird, der wegen seiner Frequenzunabhängigkeit (in Abb. 30) als horizontale Gerade
   Z ≈ Z₂ = R_E
   erscheint.
3. hohe Frequenzen (≥ 10⁶ Hz)
   Grundsätzlich kann bei weiter steigender Frequenz der zu R_E parallel liegende kapazitive Widerstand
   Z₃ = 1/ωC_E
   ein weiteres Absinken des Scheinwiderstandes bewirken solange bis schließlich der induktive Widerstand
   Z₄ = ωL
   dominierend wird und in Abb. 30 als eine "unter 45⁰ steigende" Gerade erscheint.

Die (vektorielle) Addition der je nach Frequenz sehr verschieden wirksamen Komponenten Z₁ ... Z₄ ergibt die in Abb. 30 durchgezogene Kurve Z (f) mit den ausgezeichneten Punkten

• A (f = 1/(2πR_E C₀) ; Z= R_E)
• B (f = 1/(2πR_E C_E) ; Z= R_E)
• C (f = 1/(2π√LC_E) ; Z= √L/C_E )

Der Resonanzeffekt bei Punkt C tritt allerdings bei heutigen Elektrolytkondensatoren aus folgenden Gründen nur noch in seltenen Fällen auf:

• Die in Abb. 30 (willkürlich) gewählte "Gerade" Z₁ = 1/ωC₀ entspricht einer Kapazität von etwa C₀= 20 μF.
• Ein solcher Wert liegt am unteren Ende des für Elektrolytkondensatoren (im Niedervolt-Bereich) typischen Kapazitäts-Spektrums. Bei (erheblich) größeren C₀-Werten verschiebt sich jedoch Z₁ = 1/ωC₀ eventuell um mehrere Größenordnungen parallel zu niedrigeren Frequenzen und Z-Werten unter mehr oder weniger starker "Mitnahme" der horizontalen Komponente Z₂ = R_E (Pfeile in Abb. 30).
• Die hochaufgerauhte Ätzfolie ergibt gleichzeitig mehr Kapazität pro (geometrischer) Fläche, was zu einem erheblich größeren Unterschied zwischen C₀ und C_E führt als in Abb. 30 angedeutet ist.
• Da aber andererseits Z₄ = ωL wegen des weitgehend konstanten Wertes L von diesen Konstruktionsmerkmalen kaum berührt wird, ergibt sich für den Scheinwiderstandsverlauf Z(f) des "rauhen" Elektrolytkondensators mit nicht zu kleiner Kapazität eine Kurve, die den durch C_E verursachten Resonanzeffekt nicht oder nur sehr schwach zeigt, da der durch Z₄ = ωL verursachte Z-Anstieg bereits bei Frequenzen erfolgt, bei denen C_E noch keinen merklichen Einfluß hat.

Der weitaus größte Teil der heute verwendeten Elektrolytkondensatoren kann daher durch eine weiter vereinfachte Ersatzschaltung nach Abb. 31 (ohne CE) dargestellt werden.

Abb. 31

 

Aus ihr läßt sich nun auch leicht die Temperaturabhängigkeit des Scheinwiderstandes Z (δ) ableiten, die um so stärker ist, je mehr Z durch R_E bestimmt wird, da R_E die einzige temperaturabhängige Größe in dieser Ersatzschaltung ist.

Die stärkste Temperaturabhängigkeit wird deshalb der Scheinwiderstand bei mittleren Frequenzen (Größenordnung 10⁴ Hz) zeigen. Deshalb hängt es ganz wesentlich von der Art des verwendeten Betriebselektrolyten ab, ob ein 10 kHz Scheinwiderstand z.B. bei -20⁰C auf das 3-fache oder das 10-fache seines Wertes bei +20⁰C ansteigt. (Es sei hier auf die entsprechenden Bemerkungen insbesondere im Abschnitt III.6.3 zurückverwiesen.)

Abb 32 enthält (wieder in idealisierter Form) die kombinierte Frequenz- und Temperaturabhängigkeit eines Elektrolytkondensators, dessen (willkürlich gewählte) „Gerade“ 1/ωC₀ zu einer Kapazität C₀ ≈ 16000 μF gehört. Die Lage der „Gerade“ ωL entspricht L ≈ 16 nH.

Stellvertretend für die Vielzahl der heute im Einsatz befindlichen Elektrolytkondensatoren (mit hoch aufgerauhter Ätzfolie) ist dagegen in Abb. 33 die gemessene Frequenz- und Temperaturabhängigkeit des Scheinwiderstandes Z für einen Kondensator der Kapazität C = 1000 μF und der (Nenn-) Spannung 16 V dargestellt. Die Abmessungen dieses Kondensators betragen 12 Ø x 29 mm. L beträgt 20 nH.

Es gibt zahlreiche Anwendungsfälle, in denen Elektrolytkondensatoren mit Strömen und Spannungen erhöhter Frequenz belastet werden. Die Reihe der Beispiele reicht vom Überbrückungs-Kondensator des Katodenwiderstandes im fast schon historischen Röhrenverstärker über die Frequenzweichen in Lautsprecherboxen bis zu den "sekundär-seitigen" Elektrolytkondensatoren in getakteten Netzgeräten (s. Teil V).

Dabei darf aber nicht übersehen werden, daß der weitaus größere Teil aller eingesetzter Elektrolytkondensatoren im Sinn klassischer Sieb- und Glättungskondensatoren lediglich niedrige (Netz-) Frequenzen "sieht". Daß auch für diese Kondensatoren stets die Scheinwiderstandsmessung bei erhöhten Frequenzen (typische Werte 10⁴ und 10⁵ Hz) durch einschlägige Normen und Spezifikationen vorgeschrieben ist, wird nun am Ende dieses Abschnitts verständlich:

• Eine Z-Messung bei der durch die Anteile 1 /ωC und ωL bestimmten Resonanzfrequenz
  f₀ = 1/(2π√LC)
  ergibt den Widerstand R_E, also je nach Problemstellung und Sprechweise
  die ohmschen Zuleitungsverluste oder den Wirk-Anteil oder den äquivalenten Serien-(Ersatz-) Widerstand (englisch: equivalent series resistance = ESR).

Die große Bedeutung dieses Wertes insbesondere für den Problemkreis Verlustfaktor/Wechselstrombelastbarkeit/Eigenerwärmung wurde bereits, wiederholt erwähnt.

Da die Resonanzfrequenzen ganz überwiegend im Bereich 10⁴ ... 10⁵ Hz liegen, ist die Vereinbarung bestimmter Festfrequenzen wie z.B. 10⁴ und/oder 10⁵ Hz für die Messung des Scheinwiderstandes nichts weiter als eine ökonomische (mehr oder weniger gute) Näherung für die Z-Messung bei der Resonanzfrequenz des jeweiligen Kondensators.

Die Beeinflußbarkeit des Absolutwertes R_E und damit des Minimums der Kurve Z (f) ist durch Gleichung (80)

R_E = rρ_E d/2F (80)

bereits beschrieben worden. Die wichtigsten Zusammenhänge seien hier nochmals von dieser Gleichung abgelesen:

• R_E läßt sich durch eine Verkleinerung von ρ_E herabsetzen. Das bedeutet hohe Elektrolyt-Leitfähigkeit κ_E = 1/ρ_E
  Die Leitfähigkeit läßt sich jedoch nur begrenzt steigern, da hierbei im allgemeinen die Aggressivität des Elektrolyten zunimmt (vergl. 111.6.2 und 111.6.3).
• Die Dicke d des Abstandhalters ist bei einer bestimmten (Papier-) Qualität durch eine bestimmte "Spannungsfestigkeit" vorgegeben.
  Grundsätzlich läßt sich d und damit R_E herabsetzen, wenn man gleichzeitig zu dichteren Papieren übergeht.
  Die "Spannungsfestigkeit" bleibt dabei erhalten, während die Saugfähigkeit (Speicherfähigkeit!) ab - und der Widerstandsfaktor r (III.5.3) zunimmt. Der Vorteil der kleineren Dicke d wird also durch den größeren Widerstandsfaktor r mehr oder weniger kompensiert.
• R_E läßt sich herabsetzen durch eine Vergrößerung der (geometrischen) Anodenfläche F. Das würde jedoch zunächst eine F-proportionale Kapazitätszunahme bedeuten. Da durch die jeweilige Schaltung die Kapazität aber festgelegt ist, kann die Vergrößerung von F nur erreicht werden durch Verwendung einer schwächer aufgerauhten Anodenfolie (mit entsprechend geringerer spezifischer Kapazität C_sp) oder durch eine (Vor-) Formierung der Anodenfolie mit einer Spannung, die deutlich höher ist, als im Normalfall für die Nenn- bzw. Betriebsspannung des Kondensators erforderlich gewesen wäre. ("Überformierung", Einsatz von Kondensatoren "mit höherer Nennspannung", III.1 und III.2.3).

Die hier abgelesenen Zusammenhänge sind natürlich nur qualitativ richtig, da sie noch durch zahlreiche andere Parameter beeinflußt werden. Es sei an (bereits erwähnte) Stichworte erinnert wie

• Kontaktierung des Oxyd-Dielektrikums,
• Viskosität des Elektrolyten,
• Grad und Struktur der Folien-Aufrauhung
• Imprägnier- und Formierverfahren usw. usw.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.