Realisierung von Bandpaß-Filtern in SAW Technik

• Beim FIR Filter bestimmen sich die Werte der Koeffizienten aus den Abtastwerten der Impulsantwort.
• Beim SAW Filter bestimmt sich die Länge der Elektroden ( Finger“) des IDT (interdigital transducer) aus dem Verlauf der Impulsantwort.

Wie aus diesem Beispiel erkennbar wird, können in dieser Technik "fast ideale" Frequenzgänge realisiert werden.

Die Anschlußbelegung dieses Filters:

Bei Handys und Smartphones sind für jedes der Empfangs-Bänder (3 für GSM, UMTS, LTE) entsprechende SAW Filter implementiert.

SAW Resonatoren

 

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Durch diesen Eintrag lasse ich den sehr interessanten Beitrag von Dietmar Rudolph wieder hoch kommen, weil er wichtige Ergänzungen angebracht hat.

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Im Beispiel des oben gezeigten Frequenzgangs des SAW Filters für den UKW FM Bereich sieht man, daß die Gruppenlaufzeit (group delay time) nur sehr geringe Schwankungen aufweist.

Ideal für FM sind Filter mit (absolut) linearer Phase und daraus resultierend (absolut) konstante Gruppen-Laufzeit.

Entwickler von FM Radios (aber auch von FM Sendern) müssen also darauf bedacht sein, daß die von ihnen verwendeten Filter eine möglichst konstante Gruppen-Laufzeit aufweisen.

Das führt zunächst auf die Frage, welchen Frequenzgang (Amplitudengang und Phasengang) ein Filter haben muß, damit es eine konstante Gruppen-Laufzeit aufweist. Im nächsten Schritt ist dann zu überlegen (ob und ) wie ein solches Filter tatsächlich realisiert werden kann.

Gruppen- Phasen- und Front-Laufzeiten

Bei den Laufzeiten unterscheidet man Gruppen-Laufzeit t_gr, Phasen-Laufzeit t_ph und Front-Laufzeit t_fr.

Links ist der Frequenzgang eines Tiefpasses dargestellt.

• A(ω) ist der Amplitudengang.

• Θ(ω) ist der Phasengang, wobei eine lineare Phase  Θ(ω) = ωt₀ wäre.

• ΔΘ(ω) ist die Abweichung der (tatsächlichen) Phase vom ideal linearen Verlauf.

Rechts ist ein Phasenverlauf  Θ(ω) gezeigt und verschiedene Geraden daran.

• Der Winkel bzw. die Steigung, den eine Tangente an einen Arbeitspunkt hat, ist die Gruppen-Laufzeit t_gr.
• Die Steigung einer Sehne von Ursprung 0/0 zum Arbeitspunkt ist die Phasen-Laufzeit t_ph.
• Die Steigung einer Tangente an den Phasenverlauf für hohe Frequenzen gibt die Laufzeit für die "Front" einer eingeschalteten Schwingung an.

Die verschiedenen Steigungen ergeben sich hierbei gemäß der Ableitung der Phase  Θ(ω) nach der Frequenz, z.B. t_gr = dΘ(ω)/dω.

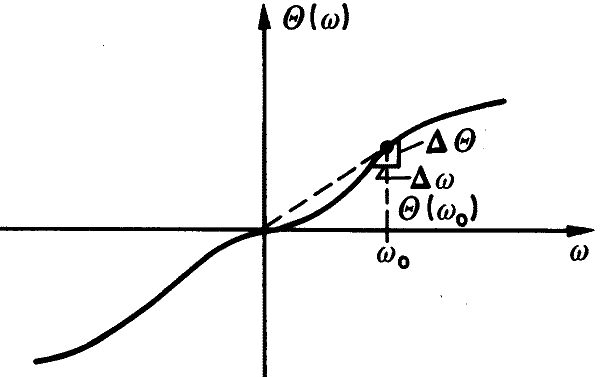
Meßtechnisch bestimmt man die Gruppenlaufzeit über den Quotienten  t_gr ≈ ΔΘ/Δω.

• Für eine einzelne Cosinus-Schwingung gibt die Phasen-Laufzeit t_ph an, um wie viel "verspätet" (also Phasen-verschoben) sie am Ausgang erscheint.
• Für eine "Frequenz-Gruppe", also für die Frequenzkomponenten, die z.B. zu einer modulierten Schwingung gehören, ist die Gruppen-Laufzeit t_gr wichtig. Diese muß für alle zugehörigen Frequenz-Komponenten gleich groß sein, damit die modulierte Schwingung am Ausgang des Übertragungs-Systems (Filters) ihre Form nicht verändert hat. (Das ist für FM wichtig.)

Verzerrungs-freies Übertragungs-System

Ideal (bezüglich der Beibehaltung des Zeitverlaufes) wäre also ein "Verzerrungs-freies" System. Dessen Ausgangs-Signal sieht - bis auf einen Amplituden-Faktor und eine zeitliche Verögerung t₀ -  genau so aus, wie das Eingang-Signal.

Ein solches verzerrungsfreies System hat also einen konstanten Amplitudengang und eine lineare Phase Θ(ω) = ωt₀. Wird ein  δ-Impuls auf seinen Eingang gegeben, so erscheint dieser nach der Zeit t₀.

Die Impuls-Antwort h(t) und die Übertagungsfunktion H(ω) = A(ω)e^jΘ(ω) hängen über die Fourier-Transformation zusammen. Meßtechnisch bestimmt man  Φ(ω) = - Θ(ω), wobei sich die beiden nur im Vorzeichen unterscheiden.

Wenn die Phase  Θ(ω) = ωt₀ einen linearen Verlauf hat, ist sowohl die Phasen-Laufzeit t_ph, als auch die Gruppen-Laufzeit t_gr konstant, wie aus der ersten Graphik hervor geht. 

Tiefpaß mit linearer Phase

Zunächst wird ein Tiefpaß mit linearer Phase betrachtet.

Dieser hat eine Impulsantwort h(t), die ihr Maximum nach der Laufzeit t₀ hat.

Die hierbei entstandene Symmetrie zur Laufzeit t₀  in der Impuls-Antwort h(t) entsteht durch die in der Durchlaß-Kurve A(ω) des Tiefpasses bezüglich   ω = 0 vorhandene Symmetrie und ist bedingt durch die Symmetrie-Eigenschaften der Fourier-Transformation.

Die Sprungantwort a(t) dieses Tiefpasses ist punktsymmetrisch bezüglich t₀ / a(∞). Die Größe t_r ist hierbei die "Anstiegszeit".

Bandpaß mit linearer Phase

Der Übergang von Tiefpaß zum Bandpaß geschieht im Frequenz-Bereich durch eine Verschiebung des Frequenzgangs um  ±Ω_c, wenn Ω_c die Mittenfrequenz des Bandpasses ist. Im Zeitbereich bedeutet das dann eine Multiplikation mit einer Trägerschwingung mit der Frequenz Ω_c. 

Der Phasen-Verlauf eines verzerrungs-freien Bandpasses muß also (ebenfalls) linear in dessen Durchlaßbereich sein, aber (als Nebenbedingung) muß seine Verlängerung die Ordinate bei ganzen Vilefachen von 2 π schneiden.

Anwendung auf SAW-Filter

Angewendet auf ein SAW-Filter bedeutet das folgendes:

• Die "Finger" seiner Struktur entsprechen den Abtastwerten der mit einer Cosinus-Schwingung auf der Mittenfrequenz Ω_c multiplizierten Impulsantwort.
• Diese Impulsantwort muß die oben gezeigten Symmetrie-Eigenschaften aufweisen und um eine Laufzeit t₀ verzögert kommen. 
• Auf Grund der Spiegel-Symmetrie der Impuls-Antwort (der "Finger") ist die lineare Phase festgelegt.
• Der Amplitudengang des Filters kann davon unabhängig festgelegt werden, ist jedoch ebenfalls Spiegel-symmetrisch (zur Mitten-Frequenz).
• Wird der Amplitudengang näherungsweise Rechteck-förmig gewählt, haben die Längen der "Finger" näherungsweise einen Verlauf wie sin(x)/x.

Die Dimensionierung eines SAW-Filters hat große Ähnlichkeit mit der Dimensionierung eines Digitalen Filters vom Typ FIR (finite impulse response).

Im Unterschied dazu haben LC-Filter keine Spiegel-symmetrische Impulsantwort, weshalb diese auch keine lineare Phase haben. Es gibt zwar Allpaß-Strukturen, mit deren Hilfe es möglich ist, die Phase zu linearisieren (Laufzeit-Entzerrer), jedoch ist eine Linearisierung des Phasengangs damit sehr aufwändig und nur näherungsweise möglich.

Literatur: Lineare Übertragungs-Systeme, Vorlesungs-Skript

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Da der Ausdruck Akustische-Oberflächenwellen-Filter im Beitrag nicht vorkommt, schreibe ich diese Zeilen. somit kann man ab morgen (Indexierung des Nachts) diesen Interessanten Beitrag auch mit dem Suchbegriff Akustische-Oberflächenwellen-Filter oder AOW-Filter bekommen - auch bei Google.

Akustische-Oberflächenwellen-Filter oder AOW-Filter sind die deutschsprachigen Ausdrücke für den SAW-Filter.

Da diese mechanischen Filter eine so grosse Zunahme erfahren haben, sollten wir diesen Bauteilen wohl einen eigenen Typ bei der Röhrensuche" geben - oder die Verwendung weiter differenzieren, um die insgesamt zu finden - mit zusätzlich "Filter" und "SAW/AOW-Filter".

Überhaupt wäre diese "Bauteile-Suche" viel besser ausbaubar - doch wer erledigt die Arbeit dazu? Das ist das Problem dabei.

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.