Aufbau und Resonanzverhalten früher ZF-Filter

1     Einführung

Die kürzliche Reparatur einiger batteriebetriebener  französischer Superhetempfänger (z.B. DUCRETET Supermodula à 5 lampes, PATHEDYNE SB) und einiger Bausatzradios aus der zweiten Hälfte der zwanziger Jahre, sowie eines französischen Superhetempfängers für Netzbetrieb vermutlich von 1933 (LAGIER ZZ) gab den Anlass, sich etwas näher mit der Schaltungstechnik dieser Gerätegeneration zu befassen. Im Zentrum des Interesses standen die aus heutiger Sicht recht ungewöhnlichen Zwischenfrequenzfilter.

Diese Empfänger entsprachen zwar in ihren Grundzügen dem Standardschema jedes Superhets: Mischstufe – Zwischenfrequenzverstärkung – Demodulation – Niederfrequenzverstärkung, jedoch zeigen sie in einigen Details überraschende Besonderheiten:

• Die Mischstufe arbeitete stets mit einer so-genannten Bi-Grille Röhre – meist mit einer A441, DZ1T, U409d, TE41 o.ä., die mit Anodenspannungen zwischen 30 und 50 V auskommen.
• Die Zwischenfrequenz lag bei 40 – 60 kHz.
  Dies ist aus heutiger Sicht schwer verständlich, da bei selbst bei guter Vorselektion die Gefahr von  Spiegelfrequenzinterferenzen besteht. Hierzu muss man sagen, dass damals so wenige Radiostationen existierten, dass Spiegelfrequenzinterferenz kaum jemals die Empfangsqualität beeinträchtigt haben dürfte.

Andererseits waren die Grenzfrequenzen der damals in der Zwischenfrequenzverstärkung ausschließlich verwendeten Trioden (RE074, A409, TA09, TA10 etc) so niedrig, dass man im Interesse ausreichender Verstärkungsreserven genötigt war, eine relativ niedrige ZF zu wählen. Weiterhin sollte in diesem Zusammenhang erwähnt werden, dass viele dieser Geräte mit einer drehbaren Rahmenantenne arbeiteten, die aufgrund ihrer Richtwirkung vielfach hilfreich hinsichtlich der Ausblendung unerwünschter Sender  war – vorausgesetzt, deren Position bezogen auf den Empfänger lag in deutlich unterschiedlichen Richtungen.

 

• Interessant ist auch zu erwähnen, dass die Mehrzahl der ZF-Filter keinerlei metallische Abschirmung aufwies. Zur Vermeidung von Stufenverkopplungen über magnetische Streufelder wurden die Filter weit voneinander entfernt angeordnet und,  insbesondere bei gedrängt aufgebauten Chassis, die Spulenachsen um 90° gegeneinander verdreht.
• Viele Geräte verwendeten noch ein Holz- oder Hartgummi (Ebonit)-Chassis und die Zwischenfrequenzfilter konnten direkt an den Wänden oder am Boden des Chassis befestigt werden, ohne das Risiko einzugehen, durch das große Streufeld der Spulen in benachbarten metallischen Strukturen Wirbelströme anzuregen, die die Induktivität der Spulen reduzieren und deren Güte senken würden. Die Situation änderte sich mit der Einführung von metallischen Chassis. Im LAGIER ZZ wurden zwar immer noch ungeschirmte ZF-Filter verwendet, jedoch wurden diese von hoch aufragenden Europasockeln getragen, um einen ausreichenden Abstand vom metallischen Chassis zu gewährleisten.
• Mit dem Ziel verbesserter Selektivität und höherer Verstärkung erfolgte die Demodulation der verstärkten ZF in vielen  Fällen mit Hilfe einer Audionschaltung. Die Rückkopplung erfolgte hierbei i.a. mit Hilfe eines Spulenvariometer (siehe z.B. Pathedyne SB, DUCRETET Supermodula à 5 lampes).
  
  
  
   
• Der Grund für die Verwendung eines Variometers für den Rückkopplungszweig des Audions dürfte darin liegen, dass eine kapazitive Rückkopplung angesichts der niedrigen Zwischenfrequenz sehr hohe Kapazitätswerte erfordert hätte.

Das folgende Bild zeigt die typische Schaltung dieser Geräte hier am Beispiel des DUCRETET Supermodula à 5 lampes. Anodenkreisleitungen sind stets fett gezeichnet.

Das von einer Rahmenantenne („cadre“) empfangene Signal wird direkt auf das Gitter 2 der Bigrille-Röhre gegeben. Im Anodenkreis der Röhre liegt in Reihe zum 1. ZF-Filter (Bandfilter mit Kreiskondensatoren von 350pF und 400pF) die Ankoppelwicklung zum Oszillatorkreis. Letzterer liegt zwischen dem Gitter 1 (Raumladegitter) und Masse.

Auf das 1. ZF-Filter folgt die einzige ZF-Verstärkerstufe. Das verstärkte Signal wird an deren Anode ausgekoppelt und auf eine Audion-Stufe mit induktiver Variometer-Rückkopplung weitergereicht. Erwähnenswert ist hierbei die Tatsache, dass die Rückkopplung nicht auf den Gitterkreis der Audionstufe selbst wirkt, sondern auf den Gitterkreis der davor liegenden 1. ZF-Röhre, bzw. den Anodenkreis des Bigrille-Mischers.

Bei dem auf die Audionstufe folgenden Transformator handelt sich um einen NF-Trafo. Der Kondensator parallel zu seinem Primärwickel dient der HF-Abblockung. Das Audio-Signal wird in einer weiteren Triode verstärkt. An der Klinkenbuchse (Jack 1 BF = Basse Frequence = Niederfrequenz) kann ein Kopfhörer angeschlossen werden. Wird Lautsprecherwiedergabe gewünscht, bleibt die Klinkenbuchse offen. Das Audio-Signal wird dann über einen weiteren NF-Trafo auf das Gitter der Endverstärkertriode geleitet, in deren Anodenleitung ein hochohmiger Lautsprecher angeschlossen werden kann.    

Der folgende Bericht beschreibt eine Anzahl von Zwischenfrequenzfiltern, die ich in den anfangs erwähnten französischen Radiogeräten meiner Sammlung vorgefunden wurden. Die Mehrzahl dieser Filter ließ sich leicht demontieren und wurde mit Hilfe zweier unabhängiger Methoden ausgemessen. Die erste Methode beschränkte sich auf die Messung von Resonanzfrequenzen mit Hilfe eines einfachen, aus wenigen Bauteilen bestehenden Exciters (Schwingungsanfachers), während die zweite, präzisere Methode erlaubte, auch frequenzabhängige Amplitudenverläufe aufzunehmen. Über deren Resultate wird in dem anschließenden Beitrag "Frequenzgänge der Bandfilter" berichtet werden.

Ein Vergleich der Resultate dieser beiden Messmethoden lässt Rückschlüsse darauf zu, in welchen Situationen eine Exciter-Messung - z.B.bei der Fehlersuche in Radiogeräten - zu einer ausreichend genauen Aussage führt, worauf bei seiner Benutzung zu achten ist, und in welchen Fällen es sich empfiehlt, zwecks Absicherung eines Messergebnisses auf präzisere Methoden zurückgreifen.

 

2     Bestimmung einer Resonanzfrequenz mit dem „EXCITER“

2.1    Das Arbeitsprinzip des EXCITERS

Die erste Messreihe an den Filtern wurde mit Hilfe eines „EXCITERS“, also eines „Schwingungsanfachers“ durchgeführt. Der Aufbau der „Schaltung zur Anregung passiver Parallelschwingkreise“ wurde angeregt durch einen Artikel von Ing. Günter Peltz in der FUNKSCHAU 1971 Heft 15: „Zweipolige Oszillatorschaltungen für Parallel- und Serienresonanz“.  

Bei der von Peltz vorgeschlagenen Schaltung handelt es sich um eine Erweiterung des bekannten Emittergekoppelten Differenzverstärkers (Abb. 18.10 aus Tietze-Schenk), bei dem das Signal vom Kreishochpunkt über einen Emitterfolger (Impedanzwandler) niederohmig ausgekoppelt wird. Hierdurch werden auch bei längeren (koaxialen) Zuleitungen zum Oszillographen oder Frequenzmesser die Rückwirkungen auf den zu messenden Schwingkreis niedrig gehalten.

Im jetzigen Aufbau fanden Transistoren des Typs BF173 Verwendung, jedoch sind auch andere HF-Transistoren mit einer Transitfrequenz von einigen 100 MHz verwendbar. Der variable Widerstand in der gemeinsamen Emitterleitung wird so eingestellt, dass der Schwingkreis gerade oszilliert. Bei zu geringem Widerstandswert von R1 werden die Transistoren zu weit durchgesteuert und verändern ihre Impedanz so stark, das die Schwingfrequenz des zu prüfenden Kreises verfälscht wird.
Der besondere Charme dieser Schaltung gegenüber anderen möglichen Schaltungen zur Anregung von Schwingkreisen basiert auf 4 Punkten:

• Es werden keine Kopplungselemente mit frequenzabhängiger Impedanz verwendet.
• Extrem geringe Anzahl von Bauelementen
• Niedrige Betriebsspannung;  beim jetzigen Aufbau 1,2V (NiCd-Aklku)
• Niedriger Stromverbrauch <1mA

Der EXCITER erwies sich allgemein als äußerst praktisches Hilfsmittel bei der Fehlersuche in Radiogeräten, insbesondere dann, wenn trotz Erneuerung sämtlicher offensichtlich defekter Bauteile ein Gerät zu geringe Selektivität oder Empfangsempfindlichkeit zeigte. Fehler in den frequenzbestimmenden Komponenten konnten durch Vergleich der mit dem EXCITER gemessenen Schwingfrequenz mit der Sollfrequenz meist problemlos identifiziert werden. Die Komponenten konnten hierbei ohne jegliche Demontage  im Gerät verbleiben, was sich insbesondere bei Messungen in Geräten mit gedrängtem Aufbau als sehr vorteilhaft herausstellte.
Obwohl die nutzbare Frequenzobergrenze von Peltz mit über 100 MHz angegeben, muss man im praktischen Einsatz bedenken, dass die durch den EXCITER in den Kreis eingebrachten Impedanzen mit steigender Frequenz zunehmend die angezeigte  Resonanzfrequenz beeinflussen.

2.2    Der praktische Aufbau des EXCITERS

Die gesamte Schaltung incl. NiCd-Akku wurde in einem Tastkopfgehäuse untergebracht:

Der Innenaufbau erfolgte auf einer einseitig durchgehend kaschierten Europa-Lochrasterkarte, sodass eine definierte Masseebene gewährleistet war. Die 3 Transistoren stecken über Kopf in der Karte.
 

Messung eines Filters Fabrikat GAMMA:
Oszillograph: Vert 200mV/div, Zeitbasis 5µs/div                     Frequenzmesser: Torzeit: 100ms
 

 

3     Die untersuchten Filtertypen

a)    Fabrikat „GAMMA“ – Hersteller von HF-Komponenten für Eigenbauradios

Stark gekoppelter ZF-Transformator (k=0,5) mit Kreuzwickelspulen, Sekundärseite (obere Spule) mit Hilfe eines Parallelkondensators von 225 pF (Glimmer) fest auf nominell 55 kHz abgestimmt. (Aufschrift: 'ACCORDÉ SUR 55KC')
Deckplatten: Ebonit, Hüllzylinder: Zelluloid, 4-poliger Europasockel

Mit EXCITER gemessene Resonanzfrequenz der Sekundärseite: 51kHz.

b)    Fabrikat „SOLENO“ – Hersteller von HF-Komponenten für Eigenbauradios

Stark gekoppelter ZF-Transformator (k=0,71) mit wild gewickelten Spulen auf Hartgummikörper. Verglichen mit den anderen hier beschriebenen Filtertypen stellt der SOLENO insofern eine Besonderheit dar, als seine Sekundärseite durch einen in den Filterkörper integrierten Trimmkondensator auf unterschiedliche Resonanzfrequenzen abgestimmt werden kann. Der mit R&S KARU gemessene Variationbereich dieses Trimmkondensators liegt zwischen 135pF und 500pF, Die Tatsache, dass nur der obere Kapazitätswert mit den auf der Abdeckplatte des Trimmkondensators aufgedruckten Werten (C=0,01 - 0,5nF) übereinstimmt, dürfte darauf zurückzuführen sein, dass das Plattenpaket bei Lösen der Stellschraube nicht mehr so weit auffächert wie zum Produktionszeitpunkt.

Mit EXCITER gemessener Resonanzfrequenzbereich der Sekundärseite: 41 – 77kHz

Man fragt sich, inwieweit dem Hersteller dieser Komponenten "SOLENO" bewusst war, welchen komplexen Einfluss die zur besseren ZF-Stufenentkopplung eingeführte metallische Abschirmung auf die Induktivität und in geringerem Maße auch auf die Güte der Spule hatte. Um einen Eindruck von der Größenordnung des Einflusses der Abschirmung auf die Spuleninduktivität zu gewinnen, wurden am vorliegenden SOLENO Filter die Induktivitätswerte des Primär-und Sekundärwickels mit und ohne den Al-Abschirmtopf gemessen (R&S LARU) und folgende Resultate gefunden:

Primär:      ohne Absch. -> L=12,2mH ... mit Absch. -> L=10,9mH -> Reduktion = -10,7%

Sekundär: ohne Absch. -> L=33,0mH ... mit Absch. -> L=28,1mH -> Reduktion = -14,8%

Eine detaillierte Behandlung der Thematik des Einflusses von metallischen Spulen-Umhüllungen und Abstimmmitteln auf deren Induktivität findet sich im Beitrag von Dietmar Rudolph et al unter dem Thema "Abgleich von Spulen". Zur direkten Veranschaulichung wurden aus diesem Thread zwei Grafiken übernommen:

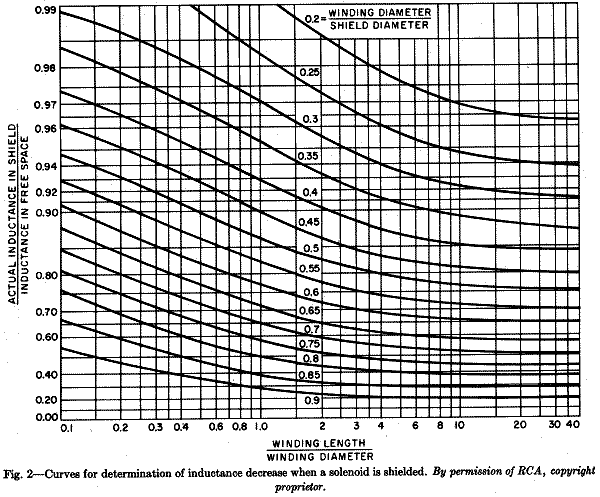
Die Kurven zeigen, daß die Abnahme der Induktivität infolge der Schirmung umso größer ist

• je dichter die Spule an der Schirmung ist und
• je länger die Spule ist im Verhältnis zu ihrem Durchmesser.

 

c)    Fabrikat INTEGRA Typ <412>

Verwendet in LAGIER ZZ. Schwach gekoppeltes Bandfilter (k=0,09) mit Kreuzwickelspulen und oberhalb des Spulenturms auf Distanzbolzen gehaltenen  Parallelkondensatoren (Glimmer) mit einem Nennwert von 500pF. Nachmessen der Kapazitätswerte mit R&S KARU ergab 495 und 480pF.
Deckplatten: Hartgummi (Ebonit), Umhüllung: Zelluloid. 4-poliger Europasockel  

Mit EXCITER gemessene Resonanzfrequenzen: Primär: 61,9kHz, sekundär: 67,3kHz.


d)    Fabrikat INTEGRA Typ <406>

Verwendet in LAGIER ZZ. Tiefpass π-Filter bestehend aus einer Längsinduktivität aus Kreuzwickelspulen mit L=63 mH und oberhalb des Spulenturms auf Distanzstangen gehaltenen  Filterkondensatoren (Glimmer) mit einem Nennwert von 4 nF zur Abtrennung der HF zwischen der Demodulatorröhre und NF-Übertrager. Nachmessen der Kapazitätswerte  ergab 3,9nF und 4,2nF.

Deckplatten: Ebonit, Umhüllung: Zelluloid. 4-poliger Europasockel

Mit EXCITER gemessene Grenzfrequenz: 14,2 kHz,

Der Kennwiderstand des Filters liegt bei Z=2,8 kOhm

e)   PATHE Pathedyne SB

Verwendet in PATHÉ Pathedyne SB. Das Gerät ist auf einem Hartgummi-Chassis (Ebonit) aufgebaut. Herstellungszeitpunkt Ende 1927 nach handschriftlichem Vermerk auf den Spulen: 13.12.1927, 19.12.1927 und 22.12.1927).

Hier wurde das zwischen der letzten ZF-Verstärkerstufe (Triode A409) und der Audion-Demodulatorstufe (Triode A409) liegende Bandfilter untersucht. Die Spulen dieses stark gekoppelten Filters (k=0,43) wurden "wild" gewickelt und auf einen Wickelkörper aus Pappe aufgebracht. Oben im Bild die Metall-Papier-Parallelkondensatoren des Bandfilters mit geschraubten Anschlüssen, Fabrikat "V. ALTER" mit nominellen Werten von Primär 250pf, sekundär 350pF (ungewöhnliche Kennzeichnung: der Kapazitätswerte: 3,5/10000 µF bedeutet 350pF)
Nachmessen der Kapazitätswerte zeigte, dass sich diese im Lauf der vergangenen fast 90 Jahre signifikant verändert hatten: Primär: 215pF, sekundär 290pF.

Der Versuch die Resonanzfrequenz der beiden Filterhälften mit dem EXCITER zu ermitteln erwies sich als problematisch. Es wurden sowohl primär als auch sekundär willkürliche Sprünge zwischen zwei definierten Frequenzwerten beobachtet: 41kHz und 65kHz. Dieses Sprungphänomen überraschte um so mehr, als die EXCITER-Messung am LAGIER <412> Bandfilter kein anomales Ergebnis produziert hatte. Zwar wurde zunächst auf einen Wackelkontakt geschlossen, dies bestätigte sich aber nach sorgfältigem Nachlöten der Verbindungen nicht. Offensichtlich handelt es sich um einen so-genannten Reiss-Effekt, der Schaltungsentwicklern in der Rundfunkindustrie sehr wohl bekannt ist, und der erstmal bereits in den gekoppelten Resonzkreisen eines frühen Radiosenders beobachtet wurde. Über die Thematik des Reiss-Effektes und die mit ihm verbundenen Probleme beim Entwurf, insbesondere der Oszillatoren, in modernen Empfängerschaltungen wird noch berichtet werden.

In parallel laufenden Untersuchungen zu den frequenzabhängigen Amplitudenverläufen dieser Filter zeigte sich, dass die beiden EXCITER-Sprungfrequenzen von 41kHz und 65kHz gerade den Höckerfrequenzen der Bandfilterkurve entsprachen. Hierüber wird später berichtet werden.

Der Grund dafür, dass der Effekt bei der EXCITER-Messung am LAGIER-Filter nicht beobachtet wurde liegt in den massiv unterschiedlichen Kopplungsfaktoren: LAGIER Integra <412>: k=0,09 PATHÉ Pathedyne SB: k=0,43.

Im vorliegenden Fall konnte der Reiss-Effekt dadurch vermieden werden, dass bei der EXCITER-Messung einer Bandfilterhälfte der Kreiskondensator von der jeweils nicht gemessenen Seite des Bandfilters abgelötet wurde. Dann ergaben sich für die Primär- und Sekundärseite des Filters "normale" (nicht springende) Resonanzfrequenzen von 48kHz bzw 49kHz.

Probeweise wurde im jetzigen Zustand - also mit den Originalkondensatoren - auch die mittlere Frequenz des gesamten Zwischenfrequenzverstärkers gemessen. Aus dem ermittelten Wert von 48,6kHz kann natürlich nur bedingt auf die ursprüngliche Zwischenfrequenz des Gerätes geschlossen werden. Nach Ersatz der Kondensatoren durch solche mit korrekten Kapazitätswerten dürfte die Mittenfrequenz etwas tiefer liegen.

 

f)    DUCRETET Supermodula à 5 lampes

Verwendet in DUCRETET Supermodula à 5 lampes. Das Gerät ist auf einem Holzchassis aufgebaut. Das Bild zeigt zwei sekundärseitig abgestimmte ZF-Transformatoren mit einem Kopplungsfaktor von k=0,25. Der rechte Transformator (1.ZF-Filter) liegt zwischen der Bi-Grille-Mischstufe und der 1.ZF-Verstärkerstufe, der linke Transformator (2. ZF-Filter) zwischen erster und zweiter ZF-Verstärkerstufe. Die Spulen sind "wild" gewickelt und auf Wickelkörper aus schwarzem Hartgummi aufgebracht.  Die Parallelkondensatoren der beiden ZF-Transformatoren werden von den zwei schwarzen, zwischen den beiden Transformatoren an die Chassisrückwand angeschraubten Blocks beherbergt. Nachmessen der Kapazitätswerte ergab 275pF für den rechten und 263pF für den linken Kondensator.

Man beachte, dass hier zum Erreichen einer induktiven Entkopplung zwischen den  beiden ZF-Transformatatoren die Spulenachsen um 90° gegeneinander verdreht wurden. Wie bereits früher in einem Beitrag von Konrad Birkner † et al erläutert, stellt sich die optimale induktive Entkopplung bei paralleler Schrägstellung der Spulenachsen um einen Winkel von 54,7°ein, dem nach dem Erfinder benannten Hazeltine-Winkel. Es bleibt im Moment ungeklärt, warum DUCRETET dieser Optimierungsvorschrift nicht folgte. Vermutlich war die Entkopplung auch bei der hier gewählten, mechanisch einfacheren Montage  ausreichend. Auch die Fälligkeit von Lizensgebühren bei der kommerziellen Verwendung der in der Hazeltine'schen Patentschrift angebenen Verfahrenweise dürfte ein Grund dafür gewesen sein, eine andere Lösung zu suchen.

Alle ZF-Transformatoren wurden mit dem EXCITER ausgemessen und ergaben die folgenden Resonanzfrequenzen: 1. ZF-Filter: 53,4kHz, 2. ZF-Filter: 58,3kHz, 3. ZF-Filter (nicht im Bild): 57,8kHz.

Eine Durchgangsmessung des gesamten ZF-Verstärkers ergab ein Maximum bei 54,3kHz.

4     Zusammenfassung der Messergebnisse

Während die einfachen Resonanzfrequenzmessungen mit Hilfe des EXCITERS an allen zuvor aufgeführten Filtertypen durchgeführt wurden, beschränkten sich die Messungen der frequenzabhängigen Amplitudenverläufe, über die separat berichtet wird, auf die Filtertypen a) - e). Von einer für die letzteren Messungen notwendigen Demontage der Filter aus dem DUCRETET wurde mit Rücksicht auf die Erhaltung des Originalzustandes des Gerätes abgesehen.

Die unten stehende Tabelle fasst noch eimal die z.T bereits bei der Beschreibung der verschiedenen Filtertypen aufgeführten Resultate systematisch zusammen. Zwecks besserer Übersichtlichkeit der Resultate wurden diese nun für die "Sekundär abgestimmte Transformatoren" und die "Bandfilter" separat gruppiert. Am Ende der Tabelle erscheint das Resultat des zu keiner der beiden Gruppen gehörenden Tiefpass-π-Filters INTEGRA <406>.

Die Spalten der Tabelle zeigen die folgenden Parameter:

• Die Induktivität der Primär- und Sekundärspule; zwecks Ermittlung des Kopplungsfaktors "k". wurde der Wert jeweils mit offener (L_offen) und kurzgeschlossener Gegenseite (L_kurz) gemessen
• Im Fall des INTEGRA Tiefpass-π-Filters die Längsinduktivität.
• Die Kapazität des extern angeschlossenen Parallelkondensators C_parallel . Hier wurden nicht die nominellen Werte der Kondensatoren angegeben, sondern die jetzt ermittelten.
• Der Ohmsche Widerstand R der Primär- und Sekundärspule
• Die mit dem EXCITER gemessene Oszillationsfrequenz des Primär-und Sekundarkreises
• Die theoretische Resonanzfrequenz des Kreises berechnet mit Hilfe der Thomson’schen Schwingungsgleichung aus den gemessenen Werten für L_offen und C_parallel

Induktivitätsmessungen erfolgten mit R&S LARU, Kapazitätsmessungen mit R&S KARU.

 

(i) Die EXCITER-Messungen an den ausgewählten ZF-Filtern ergaben Resonanzfrequenzen zwischen etwa 40 – 80 kHz.

(ii) Abweichungen zwischen den mit dem EXCITER gemessenen Resonanzfrequenzen und den theoretischen Vorhersagen sind in den meisten Fällen eine Folge der Wickel-Eigenkapazität. (Bei den berechneten Resonanzfrequenzen wurden nur die Werte der externen Kondensatoren C_parallel berücksichtigt) Während die Wickel-Eigenkapazität bei Kreuzwickelspulen im Bereich um 10pF liegt, ergeben sich bei "wild" gewickelten Spulen wie denen des Pathedyne-SB Werte bis zu 100pF!

(iii) Es mag verwundern, dass bei den "Sekundär abgestimmten Transformatoren"  auch Resonanzfrequenzen für die Primärwickel angegeben sind: 467 und 468kHz. Diese Werte ergeben sich tatsächlich bei der Messung mit dem EXCITER und entstehen durch Resonanz der Induktivität der Spulenwickel mit ihrer eigenen Wickel-Kapazität. Dies hat aber keine praktische Bedeutung, da die Resonanz infolge der Bedämpfung durch den parallel zum Primärwickel liegenden Innenwiderstand der Verstärkerröhre unterdrückt wird.

Der Grund für die auf der Primärseite des 1. ZF-Filters im DUCRETET gemessene Resonanz von 72kHz konnte bisher nicht geklärt werden.

(iv) Im Fall des stark gekoppelten Bandfilters aus dem Pathedyne-SB (k=0,43) konnte mit dem EXCITER keine eindeutige Resonanzfrequenz gefunden werden. Der angezeigte Wert sprang stochastisch zwischen 41 und 65kHz (Tabellenwerte in Klammern). Diese Werte entsprechen den bei der Messung der frequenzabhängigen Amplitudenverläufe gefundenen Höckerfrequenzen des Bandfilters!  Es scheint somit gesichert, dass es es sich hier um einen so-genannten Reiss-Effekt zwischen zwei gekoppelten resonannten Kreisen handelt. Erst wenn man den Kreiskondensator vom jeweils nicht gemessen Wickel trennt, zeigt sich bei der Messung mit dem EXCITER ein normales Resonanzverhalten ohne stochastische Sprünge, wobei die angezeigtenen Frequenzen (Werte vor den Klammern) nun wieder recht gut mit der theoretischen Vorhersage auf der Basis von L_offen und C_parallel übereinstimmen.

(v) Im Fall des Tiefpass-Pi-Filters INTEGRA <406>wurde mit dem EXCITER über der Längsinduktivität gemessen. Die Kondensatoren beidseitig der Induktivität waren somit aus der Sicht des EXCITERS in Reihe geschaltet. Entsprechend wurden bei der Berechnung der theoretischen Resonanzfrequenz L=63mH und C=C1 x C2 / C1 + C2 = 2030pF eingesetzt.  Die so ermittelte Grenzfrequenz des Tiefpass-π-Filters liegt bei 14,2kHz

5     Schlussfolgerungen

Die hier berichteten Untersuchungen haben gezeigt, dass der EXCITER ein leicht aufzubauendes und praktisches Hilfsmittel für die überschlagsmäßige Bestimmung von Schwingkreis-Resonanzfrequenzen ist und dass die Ergebnisse i.a. mit den bei den Messungen frequenzabhängiger Aplitudenverläufe gefundenen Peakfrequenzen zufriedenstellend übereinstimmten.

Nur bei den Resonanzfrequenzen der Primärwickel von nur sekundär durch parallel geschaltete externe Kondensatoren abgestimmten ZF-Transformatoren werden bei den Messungen mit der Dip-Probe z.T. niedrigere Resonanzfrequenzen registriert. Dies ist eine Folge der durch die Dip-Probe in den Messkreis eingebrachten höheren Kapazität (man muss bedenken, dass in diesen Fällen die Resonanzfrequenz durch die z.T. sehr niedrige Eigenkapazität der Schwingkreispulen bestimmt wird und dass bereits sehr kleine zusätzliche Kapazitäten die Resonanzfrequenz drastisch erniedrigen). Im praktischen Schaltungsaufbau ist der Effekt jedoch irrelevant, da der realtiv niedrige Innenwiderstand der damals als ZF-Verstärkerröhren verwendeten Trioden die Resonanz der Primärseite wegdämpfte.

Die Messungen haben bestätigt, dass die Resonanzfrequenzen der französischen ZF-Filter aus der 2. Hälfte der zwanziger Jahre eine Bereich von etwa 40 – 80 kHz überstreichen. Es ist geplant, in der französischen Fachliteratur zu recherchieren, um den Grund für die bei den verschiedenen Herstellern unterschiedlich gewählten Zwischenfrequenzen zu finden.

Es wurde demonstriert, dass es in Fällen gekoppelter Schwingkreise  vorkommen kann, dass der EXCITER keine eindeutige Anzeige der Resonanzfrequenz liefert, sondern die angezeigte Frequenz stochastisch zwischen zwei Werten schwankt. Diese Werte wurden bei den frequenzabhängigen Amplitudenmessungen (Folgebeitrag) als die Höckerfrequenzen der Bandfilterkurve identifiziert. Das Phänomen der springenden Frequenz ist als so-genannter Reiss-Effekt bekannt. Über die Implikationen dieses Effektes für die moderne Schaltungsentwicklung - insbesondere für die Auslegung von Oszillatorschaltungen - wird in einem weiteren Beitrag berichtet.

Bei Messungen an gekoppelten Schwingkreisen ist somit die vom EXCITER angezeigte Frequenz mit entsprechender Vorsicht zu behandeln und durch zusätzliche Messungen abzusichern. Dies kann z.B. dadurch erfolgen, dass man die nicht gemessene Hälfte eines Bandfilters entsprechend bedämpft (standardmäßig durch eine Serienschaltung bestehend aus Trennkondensator  + Widerstand (4,7-10nF +10KΩ) oder den Kreiskondensator von dieser Seite entfernt (was sich bei modernen, kompakten Filtergebilden schwierig gestaltet) oder den frequenzabhängigen Amplitudenverlauf misst.

Hinsichtlich des Aufbaus des EXCITERS wäre zu erwägen, ob die jetzt verwendeten Transistoren vom Typ BF173 durch solche ersetzt werden, die sich hinsichtlich der Imaginärteile ihrer Vierpol-Koeffizienten besser für einen Einsatz des EXCITERs bei höheren Frequenzen eignen.

Alternativ könnte man sich vorstellen, die Schaltung des EXCITERs dahingehend zu ändern,  dass man an Stelle der 3 Transistoren einen „Low Power Voltage Controlled Oscillator“ z.B. vom Typ MC12148 einsetzt.
Es wird weiterhin erwogen, den EXCITER mit einem kompletten PIC 16F628A gesteuerten Zählerbaustein zu kombinieren. Damit erübrigt sich der Einsatz eines  externen Frequenzmessers. Solche Zählerbausteine mit einem Messbereich von 1Hz-50MHz sind bereits sehr kostengünstig zu erhalten und könnten mit dem EXCITER zu einer Baueinheit zusammengefasst werden – z.B. durch „Piggy-Back“ – Montage des EXCITERs auf der Rückseite des Zählerbausteins.

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

Bei der Messung der ZF Bandfilter der frühen französichen Super mit Hilfe des Exciters ergaben sich im Falle von ZF Transformatoren, die nur auf der Sekundärseite als Schwingkreis ausgebildet waren, für die Primärseite Resonanzfrequenzen, die völlig von den nominellen Werten abwichen. Dies betrifft die ZF Transformatoren von GAMMA und SOLENO, sowie das PATHEDYNE ZF Filter, wie der Tabelle in Post #1 zu entnehmen ist.

Das war der Anlaß dazu, für die ZF Filter bzw. ZF Transformatoren die Frequenzgänge zu messen. Hierfür wurden folgende Methoden verwendet.

1. Messung des (betragsmäßigen) Impedanzverlaufs über der Frequenz mit Hilfe eines Dip-Zusatzes
2. Messung des (betragsmäßigen) Frequenzganges im Wobbel-Betrieb

Der Dip-Zusatz

Bei dem Dip-Zusatz handelt es sich im Prinzip um eine aktive Tastspitze (z.B. für ein Oszilloskop), die zusätzlich eine Einkopplung für einen Signal-Generator enthält.

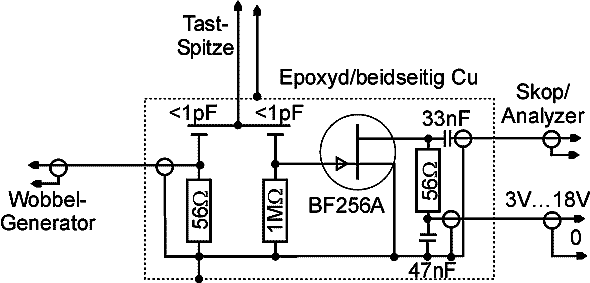
Wird als Signal-Generator ein Wobbel-Generator verwendet, kann auf dem Skop der (betragsmäßige) Verlauf der Impedanz des Meßobjektes (z.B. eines Schwingkreises) abgebildet werden.

Die gesamte Schaltung findet in einem Stück 15mm Cu Wasser-Rohr Platz.

Die Stomversorgung erfolgt aus einem (einfachen) Stecker-Netzteil und die (dünnen) BNC-Kabel für den Generator und das Skop sind fest mit dem Dip-Zusatz verbunden. Die Ein- und Aus-Koppel Kondensatoren werden aus Belägen der doppelt kaschierten Epoxyd Platte gebildet.

Im Prinzip kann statt einem solchen Dip-Zusatz auch eine aktive Tastspitze und eine Signal-Einkopplung über einen 1pF Kondensator (z.B. Signal-Leitung nur in der Nähe) verwendet werden.

Besonders bequem ist die Arbeit mit dem Dip-Zusatz, wenn ein Specki mit eingebautem Signalgenerator zur Verfügung steht. Vorteilhaft dabei ist, daß sich die Meßkurven dann gleich im logarithmischen Maßstab darstellen lassen, wodurch die Verhältnisse im Sperrbereich besser zu sehen sind.

Der GAMMA ZF Transformator

Zuerst wurde der Gamma ZF Transformator untersucht.

 Zur Messung der Induktivitäten und des Kopplungsfaktors mußte der 225pF Schwingkreis-Kondensator (von der großen Spule) abgelötet werden. (Andernfalls mißt man nicht die Spule alleine.)

Als Meßgeräte wurden hierzu verwendet:

1. Resonanz-Meßgerät "LARU von R&S" & digitales Ohm-Meter
2. Universal-Tester "LCR-T5 Multifunction Tester" (Werte in Klammer)

In einem Radio mit Trioden (kleiner Innenwiderstand) als Verstärker ist die kleine Spule L₁ in die Anodenleitung geschaltet, während der Schwingkreis mit der großen Spule L₂ den Gitterkreis der nachfolgenden Stufe bildet.

Die gemessenen Werte der Induktivitäten sind (Die andere Spule ist jeweils offen):

L₁ = 9,35mH (9,1mH)        R₁ = 103,5 Ω (105,3 Ω)
L₂ = 40,6mH (40,8mH)      R₂ = 250,2 Ω (254,8 Ω)

Wie man sehen kann, stimmen die gemessenen Werte nach beiden Methoden gut überein.

Zur Messung des Kopplungsfaktors der beiden Spulen wurde die Methode mit der L-Messung einer Spule mit kurzgeschlossener anderer Spule angewendet.  Man findet dies im Thread "Berechnungen in der Radiotechnik".  (Werte LCR-T5 in Klammer)

L₁ = 7mH (7,1mH) mit L₂ kurzgeschlossen
L₂ = 30,5mH (31,3mH) mit L₁ kurzgeschlossen

Aus den im zitierten Thread gegebenen Kurven

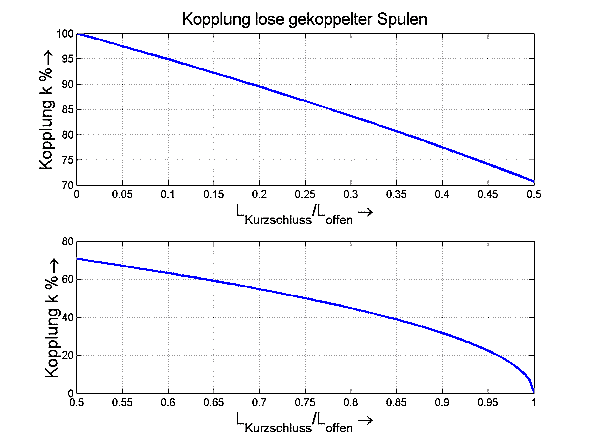
findet man so mit hinreichender Genauigkeit einen Kopplungsfaktor k = M/(L₁L₂)^½ ≈ 50%.

Die Frequenzgänge der Impedanz

Messungen mit dem Dip-Zusatz

• Dip L₁ mit L₂ offen, ohne Kreis-C

Hier erkennt man deutlich zwei Maxima. Da das Maximum bei 418,5 kHz höher ist, schwingt der Exciter dann bei dieser Frequenz. (Ein Vergleich mit den Werten aus der Tabelle (467 kHz) zeigt, daß der Dip-Zusatz hier eine deutliche kapazitive Last darstellt.) Der so gemessene Verlauf der Impedanz der Spule L₁ läßt jedoch erkennen, daß der Lastwiderstand der Triode recht kompliziert ist und es kann auch als Hinweis dafür dienen, daß solche Stufen mitunter auf völlig unvorhergesehenen Frequenzen schwingen können.

 

• Dip L₁ mit L₂ kurzgeschlossen (ohne C)

 

Der Impedanzverlauf hat jetzt nur noch eine Resonanz-Spitze. Es entspricht der unteren aus dem vorherigen Bild (die Induktivität ist ja kleiner durch den Kurzschluß), während die obere Resonanz-Spitze nicht mehr da ist. Diese kam offensichtlich aufgrund der Verkopplung mit der leerlaufenden Sekundärspule zustande.

 

• Dip L₂ mit L₁ offen (ohne C)

 

Hier ist nur noch eine Resonanz-Spitze zu sehen, die durch L₂ und die (unvermeidlichen) Schaltkapazitäten bestimmt ist.

 

• Dip L₂ mit L₁ kurzgeschlossen (ohne C)

 

Durch den Kurzschluß der Spule L₁ erniedrigt sich die Induktivität von L₂, weshalb die gemessene Resonanz-Spitze jetzt höher liegt.

Aber eine wesentliche Beeinflussung der beiden letzten Impedanzverläufe durch die Spule L₁ ist im Unterschied zum umgekehrten Fall (die ersten beiden Bilder) nicht erkennbar.

 

• Dip L₁ mit L₂ offen, aber mit Kreis C

 

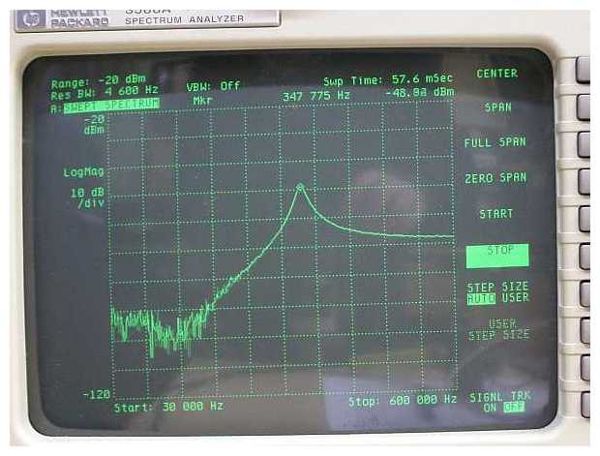
Hier ergibt sich ein Impedanz-Verlauf, der fast identisch ist mit demjenigen für kurz geschlossene Spule L₂. Auch hier ist die 2. Resonanzüberhöhung (wie im 1. Bild) nicht vorhanden.

 

• Dip L₂ mit L₁ offen, aber mit Kreis C an L₂

 

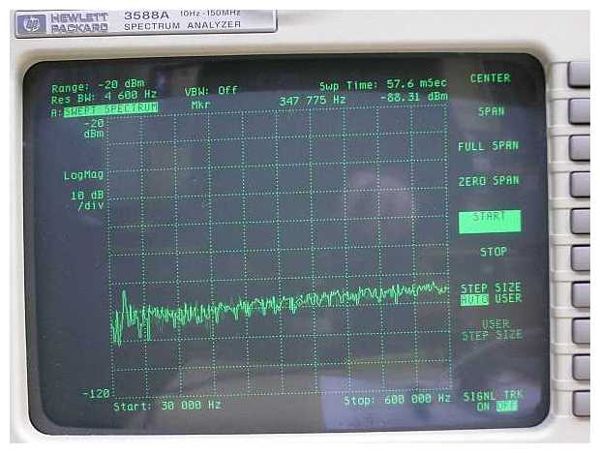
Die Einstellungen am Specki wurden hierfür gegenüber den vorherigen Messungen nicht geändert. Auf den ersten Blick hat man den Eindruck, nur noch Rauschen zu messen. Aber ganz links im Bild ist doch eine etwas höhere Spitze erkennbar. Zufall?

 

Also dann neue Messung mit anderem Frequenz-Maßstab und höherem Pegel für den Generator.

 

Und siehe da, nun läßt sich die Resonanz des Schwingkreises L₂-C eindeutig messen. Also war die Spitze in der vorherigen Messung doch kein Zufall.

 

Kontroll-Messungen ohne Dip-Zusatz

 

Hier wird der Generator direkt über 12 pF angekoppelt und mit Tastspitze (davor 2,7 pF) direkt am Schwingkreis gemessen. (Hier kann notfalls über das Ankoppel-C variiert werden. Durch die Parallelschaltung der Cs zum Kreis-C wird sich dann die Resonanzfrequenz etwas erniedrigen, aber das  ist zunächst mal sekundär.)
Hier ist eine Resonanzspitze zu sehen bei 50,8 kHz (Marker).

 

Die Messung zeigt ein ziemlich verrauschtes Bild. Aber auch bei der Messung auf dem vorherigen Bild, die zwar weniger verrauscht ist, ist keine typische Resonanzkurve eines Schwingkreises zu sehen. Das liegt daran, daß durch die kapazitive Ankopplung sowohl des Generators als auch des Speckis (am "heißen Ende" des Schwinkreises) die höheren Frequenzen bevorzugt werden. Man erhält dadurch nicht die für einen Schwingkreis typische Resonanzkurve.

 

 

Die für einen Schwingkreis typische Resonanzkurve erhält man dadurch, daß der Generator am "Fußpunkt" eingekoppelt wird. Hierfür wird dem Schwingkreis C = 225pF in Serie ein Fußpunkt C = 66 nF geschaltet und parallel zum Fußpunkt C eingespeist.
Damit wurde der Generator || zu den 66nF am Fußpunkt eingekoppelt. Messung dann mit 10:1 Tastspitze mit den 2,7pF in Serie am heißen Ende des Schwingkreises. Das gibt eine ganz saubere Resonanzkurve.

 

Messung des Frequenzgangs

 

Nun eine Frequenzgangsmessung: Generator mit 33kΩ an L₁ angekoppelt, entsprechend zum Innenwiderstand der Röhre. An den Hochpunkt vom Schwingkreis (L₂ & C =225pF) mit 2,7 pF in Serie zur Tastspitze 10:1 an Specki mit 1MOhm Eingangswiderstand gemessen. Dadurch Belastung des Schwingkreises so weit reduziert, wie es den Verhältnissen im Radio entspricht.

 

Bei einer Frequenzgangs-Messung mit Ankopplung an L₁ und Auskopplung an L₂ ist die Filterwirkung des Kreises nun deutlich zu sehen.

• Eigentlich wurde "nur" ein "einfacher" ZF Transformator vermessen. Und genau genommen interessiert vor allem sein Frequenzgang wie im letzten Bild. 
• Die vielen Messungen davor waren eigentlich nur deshalb erforderlich, weil geklärt werden sollte, wodurch die (teilweise schwer verständlichen) hohen Resonanzfrequenzen zustande kommen, die mit der einfachen und praktischen Messung mit einem Exciter zustande kommen.

Die hier an diesem Beispiel aufgezeigte Problematik findet sich entsprechend wieder bei (modernen) Halbleiterschaltungen. Die Schwierigkeit besteht dabei in der geringen Kopplung zwischen den beiden Spulen des Übertragers. Ein Beispiel aus der Praxis ist der Oszillator eines Radios mit Transistoren. Der Oszillator ist im Prinzip ja auch nichts anderes als ein Exciter, der einen Schwingkreis zu seiner Resonanzfrequenz aufschaukeln soll. Aber da die hierfür erforderlichen Koppelwicklungen stets nur kleine Koppelfaktoren haben, kann es sehr leicht vorkommen, daß die Oszillator-Frequenz (infolge einer kleinen Störung in der Versorgungsspannung) auf einen hohen Wert "springt" und dabei durch die Abstimmmittel nicht zu beeinflussen ist. Oszillatoren schwingen immer auf der Frequenz, bei der die Rükkopplungsbedingungen für sie "optimal" erfüllt sind. Solche Probleme auszuschließen ist dann das "tägliche Brot" eines Entwicklers. 

Der SOLENO ZF Transformator

Der Soleno ZF Transformator hat wie der vorherige Gamma ZF Transformator eine nicht abgestimmte Primärwicklung und eine mit einem Kondensator auf die ZF Frequenz abgestimmte Sekundärwicklung. Allerdings ist der Kondensator variabel ausgeführt, so daß sich die ZF Frequenz verändern läßt. Die Induktivitäten der Spulen und ihre Kopplung wurden hier nicht gemessen. (Messung ohne Lötkolben.)

Messung mit Dip-Zusatz

• Dip Primärspule; Sekundärkreis offen 

 

Die Messung der Primärspule zeigt (genau wie beim Gamma) ein Maximum bei einer Frequenz oberhalb der nominellen ZF Frequenz. Allerdings ist hier die (nicht gemessene) Kopplung zwischen den Spulen größer, so daß nun auch ein deutliches "Nebenmaximum" auf der ZF Frequenz (59,5 kHz) zu erkennen ist. Der Exciter schwingt allerdings auf der Frequenz des Hauptmaximums, wie aus der Tabelle in Post #1 zu entnehmen ist.

 

• Dip Sekundärkreis; Primärspule offen

 

Hier ist wieder eine Schwingkreis Resonanzkurve zu sehen, bei der der Schwingkreis im Hochpunkt kapazitiv angekoppelt ist und auch die Messung an diesem Punkt kapazitiv angekoppelt ist. Das ist beim Dip-Zusatz allerdings konstruktiv bedingt, wie aus seiner Schaltung ja hervorgeht.

 

Messung des Frequenzgangs

 

 

Die Messung des Frequenzgangs erfolgte (wieder) mit einem Generator mit Quellwiderstand 33 kΩ und am sekundären Schwingkreis ebenfalls die 10:1 Tastspitze mit 2,7pF in Serie.

Im Vergleich zum Frequenzgang des GAMMA zeigt sich, daß der SOLENO eine geringere Güte aufweist, also weniger selektiv ist. Das ist aufgrund der Art der Spule ("wild gewickelt") auch nicht anders zu erwarten.

 

Das INTEGRA <412> ZF Bandfilter

Der Typ 412 ist ein "echtes" Bandfilter mit sowohl primär, als auch sekundär abgestimmten Kreisen.

Messungen mit Dip-Zusatz

• Primärseite; Sekundärseite offen

 

Obwohl die beiden Spulen "weit" auseinander zu liegen scheinen, ist die Kopplung zwischen Primär- und Sekundärkreis noch so, daß eine überkritische Kopplung mit zwei Höckern entsteht.

 

• Sekundärseite; Primärseite offen                      

 

Auch hier sind wieder die beiden Höcker zu sehen, wobei nun der sekundärseitige das höhere Maximum zeigt.

 

• Sekundärseite; Primärseite mit 33 kΩ belastet (entsprechend zum Innenwiderstand der Röhre)

 

Der Innenwiderstand der Röhre dämpft den Primärkreis nun so stark, daß die Zweihöckrichkeit verschwindet.

Das ist (nach heutigen Maßstäben) keine optimale Dimensionierung für ein Bandfilter.

 

Frequenzgangs Messung

Die Frequenzgangs-Messung erfolgte wie in den vorhergehenden Beispielen mit Quellwiderstand 33 kΩ und Tastspitze (mit 2,7pF in Serie) am Sekundärkreis.

 

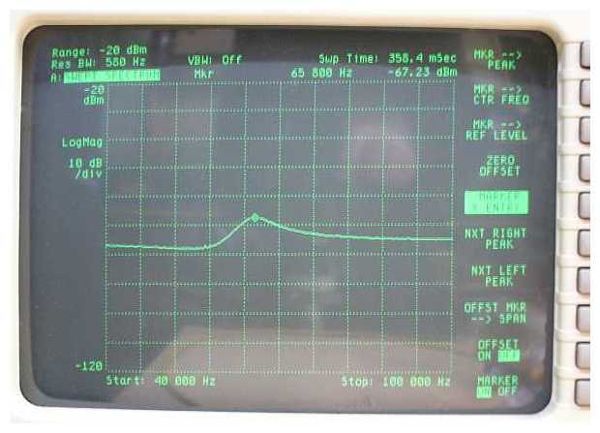
Das Messergebnis unterscheidet sich von der vorherigen Messsung mit dem Dip-Zusatz nur äußerst mariginal.

 

Das INTEGRA <406> Tiefpaß Pi-Filter

 

 

Im allgemeinen folgt auf ein Audion ein Tiefpaß (RC oder LC) um die HF abzublocken, damit diese nicht den NF Verstärker erreicht. Hier hat dieser Tiefpaß jedoch eine Pi-Struktur.

 

Netzwerke mit dieser Struktur werden i.a. als Anpaßschaltungen zwischen Sender und Antenne angewendet. Als Tiefpaß hinter einem Audion ist so eine Struktur sehr selten zu finden.

Damit ein Pi-Tiefpaß "optimal" wirken kann, muß er mit seinem Kennwiderstand auf beiden Seiten abgeschlossen werden. Gemäß der Dimensionierung des <406> ist der Kennwiderstand aber nur ca. 2,8 kΩ, was für die hier vorgesehene Anwendung eindeutig zu niederohmig ist. Man muß daher annehmen, daß die Pi Struktur nicht als NF Tiefpaß vorgesehen war, sondern "nur" zur HF Abblockung.

 

Wird als Quellwiderstand 33 kΩ gewählt und die Ausgangsseite nur hochohmig belastet, ergibt sich eine Resonanzüberhöhung bei ca. 14,1 kHz. Das entspricht auch der Messung mit dem Exciter.

Aber dieser Frequenzgang zeigt, daß sich dieses Pi Filter nicht als Tiefpaß verhält, wie man es erwartet hätte.

 

 

Wird als Quellwiderstand 8 kΩ gewählt (entspricht ca. dem Ausgangswiderstand der REN904) und als Lastwiderstand auch 8 kΩ, so ergibt sich im NF Bereich ein gleichmäßiger anstieg zu den höheren Frequenzen, womit sich der Höhenabfall infolge der geringen Bandbreite des davor liegenden ZF Filters (etwas) ausgegelichen werden kann.  

Aber im Prinzip geht dieser Ausgleich auch mit der vorherigen Dimensionierung.

 

Das Pathedyne ZF Filter

 

Das Pathedyne ZF Filter ist ähnlich aufgebaut wie die ZF Transformatoren von GAMMA und SOLENO. Auch hier zwei "wild" gewickelte Spulen zwischen Pappscheiben. Und entsprechend groß wird der Kopplungsfaktor k zwischen primärer und sekundärer Spule. Für ein "echtes" Bandfilter ist damit der Kopplungsfaktor zu groß, so daß eine stark "überkritische" Kopplung entsteht, die sich dann auch in einer Zweihöckrigkeit des Frequenzgangs zeigt.

 

Messungen mit dem Dip-Zusatz

 

Bei der Mesung mit dem Dip-Zusatz an der Primärspule zeigen sich zwei Resonanz-Spitzen. (originale C's)

 

 

Bei der Messung an der Sekundärspule sieht man wieder die gleichen Resonanzspitzen, allerdings etwas niedriger und in der Frequenz etwas verschoben.

 

Messung des Frequenzgangs

Als Schwingkreis-Kondensatoren werden (zunächst) die originalen alten Kondensatoren verwendet, deren Kapazitätswerte sich allerdings im Laufe der Zeit verringert haben (primär: 215pF [204pF] statt 250pF; sekundär 290pF [274pF] statt 350pF: Werte in [] mit Multifunktions-Tester)

• Einspeisung primär mit Quellwiderstand 82 kΩ

Man sieht hier also deutlich die beiden Höcker. Das ZF Bandfilter ist also sehr stark "überkritisch" gekoppelt. 

Der Höcker bei 65,25 kHz höher, gehört als zum (unbelasteten) Sekundärkreis.

 

• Einspeisung sekundär (82 kΩ)

Der Höcker bei 41,75 kHz gehört nun zum (unbelasteten) Primärkreis.

 

• Einspeisung primär (22 kΩ)

Die 22 kΩ entsprechen dem Innenwiderstand der Triode, an deren Anode das ZF Bandfilter angeschlossen ist.

Nun ist der Primärkreis so stark bedämpft, daß die Zeihöckrigkeit (praktisch) verschwindet und dadurch die stark überkritische Kopplung nicht mehr auffällt.

 

• Einspeisung sekundär (22 kΩ)

Bei dieser Einspeisung (rückwärts) wirkt sich die Dämpfung (fast) so aus, als wäre das Filter auf "flachen Durchlaßbereich" dimensioniert.

 

Zur Kontrolle wurden nun die Kreiskondensatoren durch die Nennwerte ersetzt:
pri. 240 pF (statt 250 pF), sec. 350 pF (Es handelt sich um neue Keramik-C's hoher Güte. Bei Messung mit KARU muß die Amplitude viel weiter zurückgedreht werden als bei den Originalen C's.) Die Resonanzfrequenzen verschieben sich dadurch zu niedrigeren Werten.

• Einspeisung primär mit Quellwiderstand 82 kΩ

 

Der Höcker des Sekundärkreises liegt nun bei 59 kHz. Die Resonanz ist hier "schärfer" als mit dem alten Kondensator.

 

• Einspeisung sekundär (82 kΩ)

 

Der Höcker des Primärkreises ist bei 38 kHz. Auch hier ist die Resonanz "schärfer".

 

• Einspeisung primär (22 kΩ)

 

Durch die Belastung des Bandfilters durch den (Innen-) Widerstand (der Röhre) wird die Zweihöckrigkeit "ausgebügelt". Das Maximum der Durchlaßkurve liegt bei 52,75 kHz.

Allerdings entspricht eine solche Dimensionierung nicht den später für Zweikreisbandfilter üblichen optimalen Anpassungs-Bedingungen. Daher erhält man auch nicht die für ein Zweikreis-Bandfilter typischen (steilen) Filter-Flanken.

 

• Einspeisung sekundär (22 kΩ)

 

Bei dieser "rückwärtigen" Einspeisung ergibt sich wieder eine Resonanzüberhöhung. Das deutet wieder auf die höhere Güte der Keramik-Kondensatoren hin.

 

Die hier gezeigte "Zweihöckrigkeit" des Pathedyne ZF Filters führte bei der Messung mit dem Exciter dazu, daß dessen Frequenz zwischen den Werten der beiden Resonanz-Spitzen (anscheinend zufällig) hin und her gesprungen ist. Dieses "Springen" der Frequenz ist ein Phänomen, das bei überkritisch gekoppelten Kreisen dann auftritt, wenn diese Teil eines Oszillators sind, wie eben beim Exciter. Mit solchen Effekten hatten auch die frühen (meist einstufigen) Rundfunksender zu kämpfen - und die anfänglichen Radios in Transistortechnik.

Bei den frühen Rundfunksendern wurde das "Springen" der Frequenz mit "Reißen" bezeichnet. Rukop hat das genauer untersucht und in einem "Reiß-Diagramm" dargestellt.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.