Messung von Induktivität & Kapazität

ID: 393145

Messung von Induktivität & Kapazität

14.Feb.16 19:55

749

Dietmar Rudolph † 6.1.22 (D)
Beiträge: 2492
Anzahl Danke: 16

Im Thread über ein L-C-Meter hat Herr Drabek zwei (hoffentlich) allgemein interessierende Fragen gestellt:

Weiss jemand wie das LARU von R&S gemessen hat?
Wissen Sie über die angewandten Methoden Bescheid (bezogen auf ein RLC Fertiggerät)?

Das LARU

Das LARU enthält (wie auch das KARU) einen Sender, dessen Skala in Induktivitätswerten (und Frequenzen) beschriftet (geeicht) ist.

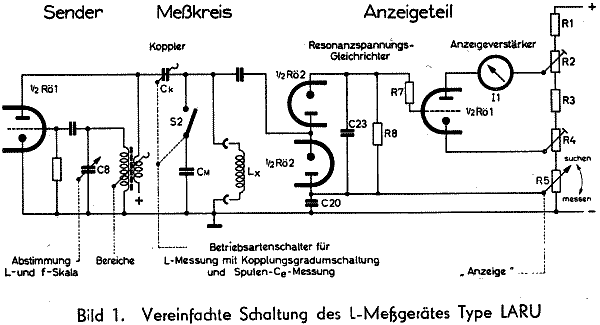
In der Triode links wird in einem Meißner-Oszillator eine HF-Schwingung erzeugt. Diese Schwingung wird über (je nach Bereich verschiedene) Koppelkondensatoren C_k an die zu messende Spule L_x angekoppelt. C_k und L_x bilden einen Serien-Schwingkreis. Im Resonanzfall (f_L) ist dadurch die Spannung an L_x maximal groß. Diese Resonanz muß mit Hilfe der Abstimmung gesucht werden. Gleichzeitig erhält man aus der Größe der Spannungs-Überhöhung im Resonanz-Punkt ein (ungefähres) Maß für die Güte der Spule.

Um die Eigenkapazität C_e der Spule bestimmen zu können, kann in einer Schaltstellung ein Meßkondensator C_M zu L_x parallel geschaltet werden. Man muß nun wieder das Maximum suchen und die entsprechende Resonanzfrequenz f_e feststellen. Hieraus berechnet sich die Eigenkapazität dann zu:

Ce/pF = 5000(f_L/f_e)² - 25

Man wendet also auch hier die Methode mit der "Pauli-Geraden" an. Eine genauere Beschreibung findet sich beim Modell.

Das KARU

Das KARU enthält ebenfalls einen Sender (wie das LARU), aber nun wird eine Meß-Induktivität L_M angekoppelt, die mit der zu bestimmenden Kapazität C_x wieder einen Serien-Kreis bildet.

Auch bei diesem Meßgerät muß nun der Oszillator so abgestimmt werden, daß eine Resonanz-Stelle gefunden wird. Auch hier erhält man aus der Größe der Resonanz-Überhöhung ein (ungefähres) Maß für die Güte der Kapazität.

Eine genauere Beschreibung findet sich wieder beim Modell.

Anmerkungen:

Das spätere transistorisierte L-Meßgerät LRT verwendet eine geringere HF-Amplitude, so daß keine Sättigungserscheinungen bei Induktivitäten auftreten können.
Das spätere transistorisierte C-Meßgerät KRT kann auch eine Vorspannung zur Messung von Elkos einstellen.
Für Messungen an Röhren-Radios sind LARU und KARU ausreichend.

Einige theoretische Betrachtungen

LARU und KARU messen Induktivität bzw. Kapazität im Frequenzbereich. Man könnte sich durchaus entsprechende Meßgeräte vorstellen, bei denen nicht von Hand abgestimmt werden muß, sondern die den entsprechenden Frequenzbereich "durchwobbeln", so daß dann die entsprechende Resonanzkurve (Durchlaßkurve) jeweils dargestellt werden könnte.

Zu einer Durchlaßkurve (Frequenzgang) einschließlich dem zugehörigen Phasengang im Frequenzbereich gehört (verknüpft über die Fourier-Transformation) im Zeitbereich die entsprechende Impulsantwort (manche sagen auch: Stoßantwort).

Der Impuls ist hierbei als δ-Impuls δ(t) definiert, also als ∞ dünner, aber ∞ hoher "Nadel"-Impuls zu verstehen, welcher so gar nicht realisierbar ist. Dieser hätte ein konstantes Spektrum für alle Frequenzen. Aber man kann sich das nun so vorstellen, daß sich ein Übertragungs-System aus diesem konstanten Spektrum genau das "herausschneidet" was seinem "Frequenzgang" entspricht. Folglich hat die "Impulsantwort" h(t) eines Übertragungs-Systems ein Spektrum H(ω), das exakt seiner Übertragungs-Funktion ("Durchlaßkurve") entspricht.

Wird der δ-Impuls integriert, so gelangt man zur Sprungfunktion σ(t). Und diese hat wieder meßtechnische Bedeutung.

Aus zwei solcher Sprungfunktionen läßt sich ein Rechteck-Impuls zusammen setzen.

Und aus Rechteck-Impulsen kann eine Rechteck-Schwingung zusammen gesetzt werden.

Messen und Prüfen mit Rechtecksignalen

Mit solchen Rechteckschwingungen, die auf Übertragungs-Systeme (speziell auf NF-Verstärker) gegeben werden, lassen sich mit Hilfe von Messungen mit dem Oszilloskop, also im Zeitbereich, die Eigenschaften dieser Verstärker im Frequenzbereich bestimmen.

Hier nur ein Beispiel dazu.

Durch Kenntnis dieser Zusammenhänge kann man sich sehr schnell einen Überblick über die Eigenschaften verschaffen. Alternativ ist die Durchlaßkurve entweder punktweise oder mit einem Wobbler aufzunehmen. Aber die hier gezeigten Kurvenformen hängen auch noch ganz wesentlich vom Phasengang ab, der mit einer punktweisen oder einer Wobbelmessung i.a. nicht zu bekommen ist.

Die Meßmethode mit den Rechtecksignalen kann daher sehr empfohlen werden.

Die digitalen Multifunktions-Meßgeräte

Ein solches Multifunktionsgerät ist heute für kleines Geld fertig aus Fernost zu erhalten.

Das Gerät mißt R, L, C, sowie Dioden, Transistoren, Triacs usw. Hier wird aber nur seine Funktionsweise für R, L, und C beschrieben.

Die zu messenden Komponenten werden hier mit einer Rampen-Spannung getestet.

Hierfür muß nun die Sprungfunktion auch noch einmal intergriert werden, so daß man zur Rampenfunktion gelangt.

Aus Abschnitten dieser Rampenfunktion kann dann eine Sägezahn-Schwingung zusammengesetzt werden. Diese Sägezahnschwingung ist nicht symmetrisch zur Nullinie, sondern stets oberhalb der Nullinie.

Zur Beschreibung der Funktionsweise genügt es, eine solche Rampenfunktion zu betrachten.

An das zu bestimmende Schaltelement wird diese Rampen-Spannung angelegt und der dabei fließende Strom gemessen.

Widerstand R: Der Strom ist proportional zur Spannung und ergibt damit eine Rampe mit einer Steigung entsprechend zum Strom.
Induktivität L: Da die Spannung an einer Spule der Ableitung des Stromes proportional ist, wird umgekehrt der Strom durch die Spule proportional zum Integral über die angelegte Spannung. Da die "Rampe" einen linearen Anstieg bedeutet, wird foglich das Integral davon eine Parabel (2. Ordnung).
Kapazität C: Da der Strom durch die Kapazität der Ableitung der angelegten Spannung entspricht, wird folglich daraus ein Sprung, dessen Höhe der Kapazität entspricht.

Aus zweien von diesen drei Anteilen setzt sich der Strom (für die hier betrachteten Fälle) zusammen:

Kondensatoren: Sprung (Kapazitätswert) & Rampe (ESR)
Spulen: Parabel (Induktivität) & Rampe (Serienwiderstand)

Die digitalen Multifunktions-Tester messen den Strom zu festgelegten Zeitpunkten. Damit erhalten sie entsprechende Punkte in der Zeit/Strom-Ebene. Durch diese Punkte wird nun eine Interpolationskurve per Rechnerprogramm gelegt. Damit erhält man die zugehörigen Koeffizienten (für die Darstellung) der Kurven. Diese Koeffizienten sind aber genau den gesuchten Werten der Bauelemente proportional.

Damit lassen sich folglich die Werte der Bauelemente bestimmen.

MfG DR

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

LC Messung mit Rampenspannungen

02.Apr.16 23:11

749 from 8474

Jochen Bauer (D)
Redakteur
Beiträge: 126
Anzahl Danke: 16

Nachdem die Methode der Induktivitäts- und Kapazitätsmessung mit Hilfe von Spannungsrampen im voraus gegangenen Beitrag von Herrn Prof. Rudolph bereits anschaulich erläutert wurde, sollen hier noch einige quantitative Betrachtungen als Ergänzung folgen.

Wir gehen dabei von einer gesteuerten idealen Spannungsquelle U aus, die eine zeitabhängige Span- nung der Form U(t)=st liefert. Dabei ist der Parameter s die Steigung der Rampe in V/s. Die Rampe beginnt bei t=0, nach Ende der Messung wird die Spannung wieder auf U=0 zurück gefahren und die Messung kann ggf. beliebig oft wiederholt werden. An diese gesteuerte Spannungsquelle wird das zu messende Bauteil angeschlossen und der resultierende Strom I(t) gemessen. Dies im folgenden Dia- gramm nochmals dargestellt:

Betrachten wir zunächst einen angeschlossenen Kondensator. Die Ladung q des Kondensators hängt bekanntermaßen mit der Spannung U am Kondensator und dessen Kapazität C über q=CU zusam- men. Da der Strom I_C(t) durch den Kondensator die erste Zeitableitung der Ladung des Kondensators ist, folgt sofort

$I(t)=I_C(t)=\dot{q}(t)=C\dot{U}(t)=C\cdot s$

Der Strom I(t) in der Messanordnung ist also in diesem Fall konstant. Aus der obigen Gleichung kann mit der bekannten Steigung s der Spannungsrampe und dem gemessenen konstanten Strom sofort die Kapazität des angeschlossenen Kondensators bestimmt werden.

Betrachten wir nun eine angeschlossene ideale Induktivität. In diesem Fall gilt natürlich gemäß dem Induktionsgesetz

$U(t)=L\dot{I}_L(t)$

woraus unmittelbar

$I(t)=I_L(t)=\int\frac{1}{L}U(t)dt=\int \frac{s}{L}t\cdot dt=\frac{1}{2}\frac{s}{L}t^2+b$

folgt. Aus der Anfangsbedingung I(0)=0 ergibt sich die Integrationskonstante sofort zu b=0. Im Falle einer idealen Spule haben wir es also mit einer quadratischen Abhängigkeit des Stromes I(t) in der Messanordnung mit der Zeit t zu tun. Durch Fitting der obigen I(t) Funktion an die über die Zeit gemes- senen Stromwerte kann wieder unter Kenntnis der Steigung s der Spannungsrampe die Induktivität L ermittelt werden.

Im Gegensatz zum Kondensator lassen sich die Verluste in einer Induktivität jedoch meistens nicht vernachlässigen, weiterhin muss in der Regel auch die Eigenkapazität der Induktivität mit betrachtet werden. Man gelangt dann zu folgender Ersatzschaltung.

Dabei ist R der Ohmsche Verlustwiderstand der Induktivität. Bei den üblichen niedrigen Steigungen der Spannungsrampe ist R praktisch der Gleichstromwiderstand der Induktivität. Der Kondensator C erfas- st die parasitäre Kapazität der Induktivität L. Aufgrund der Parallelschaltung von C zu L+R ist I(t)=I_L(t)+I_C(t), wobei I_C(t) bereits im obigen Abschnitt zu I_C(t)=sC bestimmt wurde. Es verbleibt also die Bestimmung des Stromes I_L(t) welcher durch L+R fließt.

Aus der Kirchhoffschen Machenregel ergibt sich zunächst

$RI_L(t)+L\dot{I}_L(t)=U(t)=st$

Für eine derartige Differentialgleichung 1. Ordnung mit konstanten Koeffizienten existiert ein Standard-Lösungsverfahren (siehe z.B. Meyberg, Vachenauer, Höhere Mathematik II, Springer Verlag) und die Lösung unter Berücksichtigung der Anfangsbedingung I_L(0)=0 ergibt sich zu

$I_L(t)=\frac{sL}{R^2}\left(e^{-\frac{R}{L}t}-1\right)+\frac{s}{R}t$

wie durch Einsetzen in die obige Differentialgleichung einfach nachgeprüft werden kann. Der Übergang zur Parabelfunktion im Falle von R=0 ist aus der obigen Gleichung nicht unmittelbar ersichtlich, ergibt sich aber sofort durch Einsetzen der Potenzreihendarstellung

$e^x=\sum_{k=0}^\infty \frac{1}{k!}x^k=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+...$

der e-Funktion in die obige Lösungsfunktion. Man erhält damit

$I_L(t)=\frac{1}{2}\frac{s}{L}t^2-\frac{1}{6}\frac{sR}{L^2}t^3+...$

Da hier in allen weiteren Gliedern R in höheren Potenzen im Zähler vorkommt ergibt sich für R=0 sofort die am Anfang direkt hergeleitete Parabelfunktion für I_L(t). Mit der ebenfalls bereits hergeleiteten Funk- tion I_C(t) für den Strom durch den Kondensator, welcher die parasitäre Kapazität der Induktivität dar- stellt ergibt sich nun für den Gesamtstrom sofort

$I(t)=\frac{sL}{R^2}\left(e^{-\frac{R}{L}t}-1\right)+\frac{s}{R}t+sC$

Aus dieser Gleichung ist sofort erkennbar, dass I(t) für hinreichend große Zeiten t>>R/L in eine Asym- ptotengerade A(t) der Form

$I(t)\rightarrow\frac{s}{R}t-\frac{sL}{R^2}+sC=A(t) \hspace{11pt};\hspace{11pt}t\gg\frac{R}{L}$

übergeht. Ein typischer Verlauf dieser Gesamtstromkurve I(t) sowie der Asymptotengerade A(t) ist für die Werte s=1V/ms, L=3mH, R=20Ω und C=100pF im folgenden Bild gezeigt

Prinzipiell gibt es nun zwei Möglichkeiten um aus der Messkurve I(t) die Induktivität L zu bestimmen. Zunächst könnte man versuchen durch ein Kurven Fitting zusammen mit der obigen Gleichung für I(t) bei bekanntem Parameter s die verbleibenden Parameter L, R und C zu ermitteln. In der Praxis tritt aber häufig das Problem auf, das durch den "Knick" in der Spannungsrampe bei t=0 das System zu parasitären Schwingungen angeregt wird, die durch den in der Praxis sehr geringen Ausgangswider- stand der Spannungsquelle aber schnell gedämpft werden. Im hier betrachteten Fall treten wegen der angenommenen idealen Spannungsquelle mit einem Ausgangswiderstand von exakt null keine para- sitären Schwingungen auf.

Es bietet sich daher zumindest bei Induktivitäten mit einem nennenswerten Gleichstromwiderstand von zumindest einigen Ohm folgende Methode an:

Die Messkurve von I(t) wird erst ab solchen Zeiten betrachtet, bei der sie bereits sehr nahe an der Asymptotengerade A(t) liegt. Es wird aus den Messwerten durch Fitting dann A(t) bestimmt. Aus den obigen Gleichungen ergibt sich der Schnittpunkt von A(t) mit der Vertikalachse zu

$A(0)=-\frac{sL}{R^2}+sC=-\frac{s\cdot\left(L-R^2C\right)}{R^2}$

Der Gleichstromwiderstand R der Induktivität kann sofort, wie aus dem Ausdruck für A(t) ersichtlich ist, aus der Steigung s/R der gemessenen Asymptotengerade A(t) ermittelt werden. Zur exakten Be- stimmung der Induktivität L aus A(0) würde man nun noch die parasitäre Kapazität C der Induktivität benötigen. Allerdings zeigt sich sofort, dass der Fehler in der Bestimmung von L durch Nichtbeachtung von C in der Praxis meistens völlig vernachlässigbar ist.

Dies wird Anhand eines Beispiels schnell klar. Unter Nichtbeachtung von C ergibt sich aus der obigen Gleichung für A(0) ein verfälschter Induktivitätswert von L'=L-R²C. Nehmen wir z.B. an, dass R=20Ω und C=100pF ist, so ergibt sich eine Abweichung vom tatsächlichen Induktivitätswert von lediglich L-L'=R²C=40nH absolut.

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.