Berechnungen in der Radiotechnik
Berechnungen in der Radiotechnik
In den Tabellen sind die gelben Felder Eingaben und die grünen Felder die Ergebnisse.
Ich glaube, man kann sich damit viel Rechenarbeit ersparen.
Für Anregungen und Korrekturvorschläge bin ich dankbar.
Mit Sammlergruß
D. Grötzer Anlagen:
- Eigenkap u. Ind. Spule (21 KB)
- Gleichrichter (30 KB)
- Spulen (54 KB)
- Transformatoren (26 KB)
- Schwingkreisberechnung (39 KB)
- Grundlagenberechnung (30 KB)
- Ergaenzungen (64 KB)
- Roehren (81 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Hallo Sammlerkollegen.
Nach dem meine Berechnungen in Excel positiv aufgenommen werden habe ich, angeregt von den Beiträgen über Heizungs-Vorschaltkondensatoren und Wellenwiderstand von Leitungen, diese in mein Excelprogramm aufgenommen. Viel Spaß beim Berechnen. Für weitere Anregungen bzw. Korrekturen bin ich dankbar.
D. Grötzer
Anlagen:
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.

hiermit stelle ich meine Excel-Datei zur Berechnung der Messbereichserweiterung von Strom- und Spannungsmessern zur Verfügung.
Siehe Anlage.
Viel Spaß damit, Hans-Thomas Schmidt
Edit: Schaltbilder hinzugefügt Anlagen:
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
? Bestimmung eines unbekannten Ausgangsübertrager

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Trafo ausmessen

Hallo Herr Zylka,
anbei eine Beschreibung, wg der Formeln als pdf. Mit dem Programm von Herrn Grötzer können Sie weitere Berechnungen vornehmen, weiter unten finden Sie einen Bericht von Herrn Knoll, der alle Feinheiten anspricht.
[1] Klein, Netztransformatoren und Drosseln ISBN 3-7723-1064-8 (ein einfaches nützliches Buch mit allen Tabellen. sehr zu empfehlen, falls es das noch gibt.
Gruß
Georg Beckmann
Gerade habe ich einen Fehler bemerkt und wollte die Anlage ersetzen. Das konnte ich jedoch nicht, deshalb die richtige ist Beschreibung1.
Anlagen:- Beschreibung1 (32 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Scheinwiderstand
Hallo Herr Zylka,
wie von Herrn Beckmann dargestellt kann die Induktivität des Ausgangstrafo bestimmt werde. Der Scheinwiderstand Z ist allerdings frequenzabhängig.
Z = ((R2 + (XL+ Xc)2)0,5 und XL=2*π*f*L XC= 1/(2*π*f*C) das geht klar aus der Frequenzabhängigkeit der Blindwiderstände hervor.
MfG D. Grötzer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Danke

Hallo Herr Beckmann,
herzlichen Dank für die schnelle Antwort.
Gruß
Wolfram Zylka
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Kopplung von Spulen

Bei gekoppelten Spulen lassen sich die primäre und die sekundäre Induktivität z.B. mit einem Induktivitätsmeßgerät, z.B. LARU, bestimmen.
Wie aber mißt man die Kopplungs-Induktivität M bzw. den Kopplungs-Koeffizienten k?
Dafür gibt es eine einfache Methode, die aber nicht oft beschrieben ist.
Eine frühe Quelle ist: "Benz, F.: Meßtechnik für Funkingenieure, Springer, Wien, 1952"
bzw. "ITT: Reference Data for Radio Engineers, 6th ed., Howard & Sams, 1975"

In beiden angegebenen Quellen wird die Messung von k auf die Messung der Induktivität bei offener und bei kurzgeschlossener Sekundärspule zurückgeführt. Die angegebene Formel läßt sich graphisch einfach auswerten.
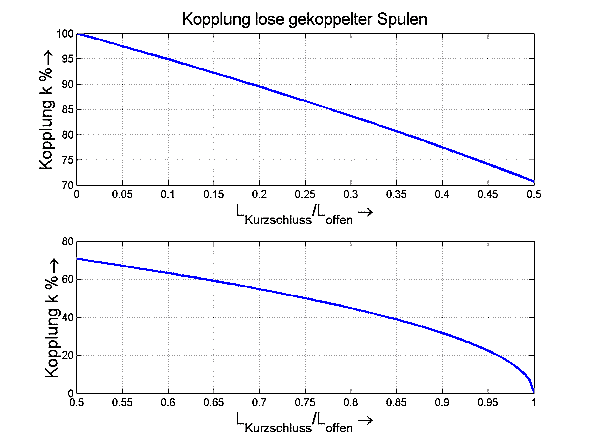
Wie Herr Knoll bestätigt hat, ist diese Messung in der Praxis ausreichend genau, vorausgesetzt, die Güte der Spulen ist nicht zu schlecht. Für Spulen von Bandfiltern (ohne die Kondensatoren) ist sie somit anwendbar.
Die Kopplungsinduktivität M ist somit M = k*(L1L2)1/2 , also: k * geometrisches Mittel aus L1L2
Vielen Dank an Herrn Knoll!
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Topfkreise

Zur Berechnung von Topfkreisen u.a. Im Handbuch für Hochfrequenz- und Elektrotechniker von Curt Rint, Band 2, Seite 437/438 finden sich allgemeine Formeln zur Ermittlung von Induktivität und Kapazität in Topfkreisen. Siehe Anlage.
Anmerkung: alle Maße (Länge, Fläche, Durchmesser d und D) sind in cm einzusetzen.
Anlagen:- Topfkreis_berechnen (52 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Nomogramm für Schwingkreise

Wer die mathematische Berechnung mit der Thomson-Formel scheut, kann sich einfach eines Nomogramms bedienen. Das ist eine graphische (grafische) Darstellung über die Verknüpfung dreier Größen.
In der Anlage ist ein solches Nomogramm zur Schwingkreisberechnung. Es zeigt Kapazität, Induktivität und Wellenlänge/Frequenz.
Auch die alten "cm"-Größen für Spulen und Kondensatoren sind berücksichtigt.
Die Genauigkeit ist natürlich nicht überwältigend, reicht aber in der Praxis völlig aus.
PS: weitere Formeln aus der Radiotechnik finden sich u.a. in "Radios von Gestern", Seite 424 u.425,
Anlagen:- Nomogramm-Schwingkreis (21 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Widerstände für LED schnell berechnen.
Ein Dankeschön für die hilfreichen Tabellen.
Dafür ist sicher einiges an Arbeit angefallen.
Ich habe mir eine Exceldatei geschrieben um zügig LED in Betrieb zu nehmen.
Recht simpel, liegt als Icon auf dem Desktop und man kann sofort arbeiten.
Vielleicht ist sie für weitere User auch ein wenig hilfreich
Gruß J.E.
Anlagen:
- LED Rechner (26 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Berechnung von Zylinderspulen

In der frühen Radiotechnik spielten einlagige Zylinderspulen als Induktivitäten von Resonanzkreisen eine wichtige Rolle. Mit dieser Spulenform ließen sich die für Resonanzkreise erforderlichen Güten
erzielen.
Mit der Erfindung von Ferriten verlor dann die Zylinderspule ihre Bedeutung, zumindest für tiefere Frequenzen und bei kleinen Pegeln. In der Sendertechnik wird sie allerdings auch heute noch verwendet, auch für Langwelle.
Betrachtet werden hier einlagige Zylinderspulen, wie diese früher z.B. bei Detektoren oder auch Audions zum Einsatz kamen.
Hierbei wird vereinfachend angenommen, daß die Wicklungsstärke gegenüber dem Durchmesser des Zylinders vernachlässigbar ist.
Auf diese Weise ergeben sich einfache Formeln zur Berechnung der Induktivität einer Zylinderspule. Da aber die magnetischen Feldlinien bei diesen Spulen eben nicht im Ferrit gebündelt und geführt werden, hat dies zur Folge, daß sich die Induktivität bei langen Zylinderspulen nicht mehr direkt proportional zum Quadrat n2 der Windungszahl n ergibt. Weiter entfernte Teile einer langen Zylinderspule sind nicht mehr zu 100% mit einander verkoppelt.
Die exakte Berechnung erfordert eine Integration über die magnetische Feldverteilung. In der Praxis behilft man sich dafür mit Kurven, die das Resultat einer solchen Berechnung sind.
In der Fachliteratur findet man hierzu entsprechende Graphiken. Allerdings sind diese bei jedem Autor anders normiert, führen aber zu gleichen Ergebnissen. Es werden drei Beispiele dazu vorgestellt.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Vorschaltkondensatoren im Heizungskreis

Ergänzend zu der Berechnungsmöglichkeit mit einer Excel-Tabelle in Post#2 wird eine graphische Berechnung aus "Springsten, K.A: Einführung in die Kurzwellen- und Ultrakurzwellen-Empfänger-Praxis, FV, 1953, S. 74" vorgestellt.
In diesem Diagramm ist die für 50Hz notwendige Größe des Vorschaltkondensators C/µF in Abhängigkeit der Summe der Heizspannungen Uh/V der in Serie geschalteten Röhren aufgetragen, wobei der Heizstrom Ih/mA als Parameter bei den Kurven angegeben ist.

Wie aus den Formeln ersichtlich ist, ist die Größe C des Vorschaltkondensators proportional zum Heizstrom Ih.
Die Größe von C für Ih = 300mA erhält man deshalb dadurch, daß die notwendigen Kapazitätswerte für Ih = 200mA und Ih = 100mA addiert werden. Auf diese Weise können auch Vorschaltkondensatoren für andere praktisch vorkommenden Stromstärken bestimmt werden.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Umrechnung: Frequenz <=> Wellenlänge

Ältere Radios haben meist Skalen, die in Wellenlängen beschriftet sind mit Angaben in Metern (m). Dagegen ist man heute eher gewohnt, in Frequenzen (kHz) zu denken. Beide Werte sind reziprok zu einander, wobei die Lichtgeschwindigkeit c noch berücksichtigt werden muß.
Da die meisten Skalen sowieso nicht so ganz genau sind, genügt es in der Praxis aber auch, wenn die "Umrechnung" mit Hilfe einer Tabelle erfolgt.
Die Tafel III stammt aus "Wiesemann, H.: Praktische Funktechnik, 2.A., Frankh, 1939".

MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Das Dezibel - dB für Dummies
Keine Angst vor dem dB!
Durch den Logarithmus werden sehr große oder sehr kleine Zahlen überschaubar. Daher greift man in der Elektrotechnik gerne zum Logarithmus, wenn es darum geht, große Zahlenverhältnisse darzustellen oder mit ihnen umzugehen.
Den 10er Logarithmus eines Verhältnisses zwischen zwei elektrischen Größen nennt man in der Elektrotechnik – zum Gedenken an Alexander Graham Bell - ein „Bel“. Da aber ein Bel noch ziemlich unhandlich ist, nimmt man stattdessen ein Zehntel eines Bel, das Dezibel.(1dB = 1/10Bel)
In dem angehängten pdf Dokument wird versucht, das so praktische "Dezibel" all denjenigen näherzubringen, für die der Umgang mit dem "dB" nicht zum täglichen Handwerkszeug gehört.
Viel Spass damit
Fred
(Falls Fehler drin sind, bitte um Nachsicht und Nachricht)
Anlagen:
- Dezibel (pdf) (252 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Leistungs- und Spannungs-Pegel; Dezibel, Dämpfung

Zu Dezibel, Dämpfung, Neper sowie Leistungs- und Spannungspegeln findet man auch einen Beitrag in "Texte".
Es wird hierbei auch auf den Unterschied von "Verstärkung" und "Dämpfung" bei den dB Werten eingegangen.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Warum ist die Schwingungsdauer im LCR Schwingkreis genau 2Pi

Wie kann man das mit den Grundrechnungsarten beweisen? Wie weiss also ein Schwingkreis mit 1H, 1F und Sereinwiderstand z.B. 1 Ohm, dass die Periodendauer 2PI = 6,28 sec dauert und sich auch die Frequenz der Schwingung ergibt, ohne die Thomsonformel zu kennen.. Im Excelblatt im Anhang können sie Werte verändern und die Auswirkungen studieren. Die Sinus und Cosinuskurve ergibt sich nur aus den bekannten Grundgleichungen C*U = i*t und L*I = u*t, die ich als bekannt voraussetze.
Motivation ist die Tatsache dass die ca. 20000 Mitglieder u.a. gerne dem Hobby Radio in vielfältigster Form frönen. Sie gehören auch Berufen an, die mit Radiotechnik wenig zu tun haben und versuche damit ihr Interesse zu wecken.

Auch mit mit Grundrechnungsarten sind komplizierte Eigenschaften darstellbar.
In den Tabellen der insgesamt drei Blätter sind nur diese verwendet worden.
Wichtig ist dabei, dass die Energiespeicherung in L und C mit dem Quadrat von I und U zusammenhängt, siehe Blatt2 des Excel. Das ergibt sich sozusagen von alleine. Und Pythagoras auch seine Rolle dabei spielt.
Erst am Ende des letzten sheets zeigt sich der Zusammenhang mit den Winkelfunktionen. Siehe Bild unterhalb.

Im Anhang noch die Exceldatei, die offen für andere Daten sind, um Einflüsse besser erkennen zu können. Die Bilder hier im Beitrag nur zur Information.
Einige Zusatzinfo siehe Profil.
- Schwingungen (137 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Frequenz der gedämpften Schwingung

Hallo Herr Drabek
An dieser Stelle ist vielleicht eine Ergänzung angebracht. Die Frequenz ω0 der ungedämpften Schwingung des LC Schwingkreises ist
Die Frequenz ωd einer gedämpften Schwingung im LCR (Serien)Kreis ist jedoch niedriger als ω0 und
beträgt
Das lässt sich durch Lösen der Differentialgleichung des LCR (Serien)Kreises leicht nachrechnen oder
auch in vielen Lehrbüchern nachschlagen. Im Falle einer geringen Dämpfung, also eines hinreichend
kleinen Widerstandes R ist die Frequenz einer gedämpften Schwingung natürlich näherungsweise durch ω0 gegeben, weswegen auf den Unterschied zwischen ω0 und ωd in manchen praktisch orientierten Büchern gar nicht erst eingegangen wird.
Wenn sie allerdings als Beispiel L=1H, C=1F und R=1Ω angeben, dann ist in diesem Fall die Frequenz der gedämpften Schwingung
was schon eine beachtliche Abweichung von ω0=1/s ist. Die Periodendauer T ist in diesem Falle
T≈7.26s anstelle von T=2π≈6.28s. Dieses Ergebnis erhalten sich auch mit ihrer Methode die
Differentialgleichung des LCR (Serien)Kreises numerisch mit der Euler-Methode über ein Excel
Sheet zu lösen. Setzt man im angefügten Excel Sheet R=1Ω, so ist die erste Nullstelle des
Stromes nach Beginn der Schwingung ungefähr bei T/2=3.6s anstelle von T/2=3.141...s
Gruß Jochen Bauer
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Einfluss der Dämpfung auf die Periodendauer

Hallo Herr Bauer
Was mich natürlich nicht verwundert ist die Tatsache der guten Ergebnisse von Differenzengleichungen anstelle der Infinitesimalrechnung. Schon bei wenigen Berechnungspunkten je Periode sind die Ergebnisse sehr genau. Darum, geplanterweise, kann man im Excel Parameter ändern. Dauerte schon viele Stunden bis das Excel fertig war. Habe gar nicht gewusst, dass das die Eulermethode ist.
Der Zweck meines Beitrages ist ja möglichst vielen Freunden des RMorg zu zeigen, dass man nicht unbedingt höhere Mathematik beherrschen muss um ein tiefes Verständnis der Vorgänge z.B. in Schwingkreisen zu erhalten. Deshalb auch der Hinweis wie durchgängig der Energieinhalt von Massen in Bewegung, Kondensator, Spule, Torsionsfeder und Spiralfeder sind. Überall kommt das Quadrat der "Aufladung" vor. So durchgängig ist die Natur. Meine Ausbildung in Mathe ist ja sehr begrenzt, Matura, aber fast nichts vergessen. Deshalb habe ich u.a. das hier gebracht um die Grundlagen zu stärken und vielleicht etwas zu initiieren.
Ich habe noch einige Beispiele im Zeitbereich durchgerechnet, die u.a. Nichtlinearitäten einschliessen.
Z.B.: TT-Glied das zeigt wie schnell es einschwingt und einen RC-Oszillator in teilweiser Übersteuerung, wo die Rechnung = Diagramm exakt dem Oszillogramm gleicht. Ich weiss gar nicht ob Spice Parameter begrenzen kann, hab es aber nicht versucht. Aber Spice ohne Hintergrund anzuwenden wäre für mich nicht sehr zufriedenstellend.
Der Punkt hier ist aber hier auch tiefere Einblicke zu gewinnen, was ja dann viel Freude macht.
LG Rudi Drabek
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Temperaturbestimmung von Trafos

Temperatur der Wicklung
Die Temperatur von Netztrafos kann entweder mittels Temperaturfühler bestimmt werden, wie diese bei (fast) jedem Multimeter verfügbar sind, oder alternativ mit Hilfe von (berührungslosen) Infrarot-Thermometern.
Die Wicklungstemperatur im Innern von Trafos läßt sich auch über zwei Widerstandsmessungen, bei kaltem Trafo und bei warmem Trafo, bestimmen.


- Man braucht also nur den Koeffizienten rδ = Rwarm / Rkalt zu berechnen und kann dann mit Hilfe der Grafik Bild 3.1/9 die Temperatur der Wicklung bestimmen.
Zur Verlustleistung
Wegen der unvermeidlichen Verluste im Transformator wird dessen Wicklungstemperatur δw, im Betrieb höher sein als die der umgebenden Luft bzw. die des umgebenden Raumes δugb. Man läßt heute als maximale Transformatortemperatur etwa δ = 100... 115 0C zu. Bei noch höheren Temperaturen werden die zur Zeit gebräuchlichen Isoliermaterialien zerstört. Die Übertemperatur δü ,
δü=δw - δugb, Gl.3.1/43
darf demnach je nach Material nicht mehr als etwa 60 ... 75 0C betragen, wenn man als maximale Umgebungstemperatur δugb max = 40 0C ansetzt.
Die Verlustleistung Pv eines Transformators setzt sich aus zwei wesentlichen Anteilen zusammen, den Eisenverlusten PE und den Kupferverlusten PCu.
PV = PE + PCu Gl. 3.1/44
Die Übertemperatur eines δü Transformators ist im Bereich von 20 ... 120 0C aus folgender Beziehung berechenbar :
δü = κ(PCU + 0,4 PE) Gl. 3.1/45
κ Wärmewiderstand des Transformators in grd/W
Lit: "Wagner, S.W.: Stromversorgung elektronischer Schaltungen und Geräte, Decker's, 1964"
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Temperaturen nach VDE0860 neu EN60065

Mit den Werten aus dem Normblatt DIN VDE0860 Seite 12, wurden zumindest bis 1989 die Geräte der Unterhaltungsindustrie entwickelt und nach VDE freigeben.
Die Werte koennen beim vorausgehenden Beitrag von Prof. D. Rudolph,angewendet werden.
Hans M. Knoll

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Serien zu Parallelwandlung von RC Gliedern und vice versa

Bei der Messung der Güte der Variometerspule wurde über einen 15 pF Kondensator angekoppelt. Da der Innenwiderstand des DDS Generators nicht Null sondern 50 Ω ist wird das Messergebnis beeinflußt. Ein Detail über diese Beeinflussung siehe hier. Wenn man also kein Laborequipment zur Verfügung hat mit 0,05 Ω Quellwiderstand und 100 MΩ Messwiderstand sondern 50 Ω und 10 MΩ muss man den Fehler berechnen können. In vielen Fällen genügt eine Abschätzung, wenn der Messfehler nur einige % groß ist.
Die gemessene Leerlaufgüte des Variometers lt. Link bei den angeführten Bedingungen ist also 69 und entspricht einem Parallelwiderstand des Schwingkriese von 52 kΩ. Die Belastung durch den Tastkopf mit 10 MΩ ist also 1:200 = 0,5%. Die 50 Ω bewirken eine Kreisbelastung von weiteren 2,2 MΩ mit 1:42 = 2,4%. Für Amateure sollte das ausreichend sein.
Wie groß ist nun der Einfluss des 50 Ω Quellwiderstandes. Man muss also die Serienschaltung von 50 Ω und 15 pF bei 1 MHZ auf eine Parallelschaltung umrechnen wie folgt:
Z = Rs + jXs Bei Parallelschaltung sieht es so aus: 1/Z =1/Rp + 1/jXp
Da Z ja in beiden Fällen gleich sein muss ist diese Gleichung zu lösen, was für interessierte hier zu sehen ist:

Bitte die Handschrift zu verzeihen. In der Anlage ein Excel, das für RC Glieder angewendet werden kann. Die Formeln, siehe oberhalb, eignen sich auch für Induktivitäten, das Excel vorerst nicht!

Da sich bei kleinen Verhältnissen von Rs, Rp zu Xs bzw. Xp bei Umrechnung der komplexe Anteil ändert ist dies bei einem Philipsgerät, Name vergessen, für eine KW-Lupe verwendet worden. Zur Veränderung der Abstimmfrequenz wurde ein Potentiometer verwendet. Herr Jochen Bauer hat dies im Thread 18 schon dargestellt warum das so ist.
Anbei das Excel für eigene Experimente.
Anlagen:
- Serie-zu Parallel (33 KB)
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Umrechnung von Serien-Schaltung in Parallel-Schaltung

Zu dieser Themenstellung findet man in der Literatur einige anschauliche Darstellungen.
Zunächst ein Text aus "Meinke, H.; Gundlach, F.W.: Taschenbuch der Hochfrequenztechnik, Springer, 1956 - 1968"

Da die Blind-Komponenten Xp bzw. Xs frequenzabhängig sind, gilt eine solche Umrechnung immer nur genau für eine Frequenz. Ändert sich die Frequenz, ändern sich nicht nur die umgerechneten Blind-Komponenten (Induktivitäten bzw. Kapazitäten), sondern auch die umgerechneten Wirk-Komponenten (Widerstände bzw. Leitwerte).
Daß sich Serien- und Parallel-Schaltung auch unterschiedlich verhalten, wenn sich die Wirk- oder die Blind-Komponente ändert, zeigt eine Darstellung aus "Lunze, K.: Theorie der Wechselstromschaltungen, 4.A., VEB Technik, 1974".

In "Henney, K.: Radio Engineering Handbook, McGraw-Hill, 1959" ist dann dargestellt, wie sich die Impedanz von Serien- bzw. Parallel-Schaltung betragsmäßig mit der Frequenz ändert. Auch daraus wird erkennbar, daß genaue Übereinstimmung immer nur bei einer Frequenz besteht.

Die bei Meinke zitierten Formeln ergeben graphisch für die Serien-Schaltung horizontale und vertikale Linien, während sich für die Parallel-Schaltung (orthogonale) Kreise ergeben, wie aus obigem Beispiel zu sehen ist.
Meinke hat nun diese Umrechnungen für (ausreichend) viele Werte gemacht und so das "Widerstands-Diagramm" erhalten.

Dieses Widerstands-Diagramm gestattet nun graphisch die Umrechnung zwischen einer Serien-Schaltung und einer Parallel-Schaltung mit für die Praxis (meist) ausreichender Genauigkeit.
Damit beliebige Werte der Widerstände berechnet werden können, sind diese jeweils so zu normieren, daß sie mit den im Widerstands-Diagramm eingetragenen Zahlen-Werten übereinstimmen.
Auf diese Art und Weise haben Ingenieure und Entwickler in der Praxis gearbeitet, bevor ein PC allgemein zur Verfügung stand.
Die Grafik hat dabei den Vorzug, daß sich Änderungen der Werte bzw. der Frequenz sehr leicht überblicken lassen. Und häufig genügt in der Praxis auch eine ausreichend genaue Abschätzung.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Resonanzfrequenz bei Verlusten im Schwingkreis

Angeregt durch die Beiträge #18 und #23 stellte sich die Frage wie sich die Resonanzfrequenz ändert bei einem Verlustwiderstand in Serie zum Schwingkreiskondensator. Es ist wohl mehr eine theoretische Frage, da üblicherweise bei C's immer von einem Parallelverlustwiderstand ausgegangen wird.
Die Beziehung für einen Verlustwiderstand in Serie zur Induktivität ist links im Bild und bekannt. Rechts die abgeleitete Beziehung für den Verlustwiderstand in Serie zur Kapazität, die mir neu ist. Die Schaltung ist auch in der LTspice Simulation zu finden.
 Sorry für die schlechte Qualität des Scans, aber die Unterschiede sind doch deutlich zu erkennen. Eine Untersuchung mit LTspice zeigt, dass die linke Formel gespiegelt bei der Resonanzfrequenz die rechte Formel ergibt, was für mich etwas überraschend war.
Sorry für die schlechte Qualität des Scans, aber die Unterschiede sind doch deutlich zu erkennen. Eine Untersuchung mit LTspice zeigt, dass die linke Formel gespiegelt bei der Resonanzfrequenz die rechte Formel ergibt, was für mich etwas überraschend war.

Nachträglich schaut alles logisch aus, da bei niedrigen Frequenzen mit R in Serie zum L sich die grüne Kurve ergibt. Die rote Kurve mit R in Serie zum C ist ja für hohe Frequenzen praktisch nur der Widerstand.
D.h. dass die, im #22 erwähnte KW-Lupe sich auch mit einem Potentiometer in Serie zu einem Teil des Oszillatorschwinkreises realisieren ließe.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
RLC HP und RLC TP 2. Ordnung

Eine "Symmetrie" des roten Frequenzgangs [Vn001] mit dem grünen Frequenzgang [Vn002] ist graphisch nur deshalb zu sehen, weil die Frequenzachse logarithmisch unterteilt ist. Bei einer linear unterteilten Frequenzachse gibt es keine Symmetrie.
Bekanntlich ist (a) y = x eine Gerade und (b) y = 1/x eine Hyperbel.
In einer doppelt logarithmischen Darstellung wird aus (a) eine ansteigende Gerade und aus (b) eine fallende Gerade. Damit hat man in einer solchen Darstellung anscheinend eine "Symmetrie".
Für Fachleute, die sich in Regelungstechnik und mit Bode-Diagrammen auskennen, kann unmittelbar der
- rote Frequenzgang einem RLC Hochpaß (HP 2. Ordnung mit Dämfung < 1) und der
- grüne Frequenzgang einem RLC Tiefpaß (TP 2. Ordnung mit Dämfung < 1)
zugeordnet werden. Wegen Dämpfung < 1 entsteht bei der "Eckfrequenz" eine Resonanzüberhöhung.
Bei der Stabilisierung von Regelkreisen haben solche Frequenzgänge der "Regelstrecke" selbstverständlich "praktische" Bedeutung.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
RLC HP und RLC TP 2. Ordnung

Man lernt nie aus. Danke schön.
Zu y=x bzw. y=1/x : Unabhängig von der Teilung der Achsen finde ich persönlich doch eine schöne Symmetrie. Nämlich:
X= ωL steigt mit 6 dB/Oktave oder 20 dB/Dekade und X=1/ωC fällt mit 6 db/Oktave, was ja nichts mit der Wahl der Achsenformatierung der Darstellung zu tun hat.
Das HP- oder TP-Verhalten eines Schwingkreises mit Verlusten war mir neu. Die Antwort ist deshalb verzögert, da ja i.A. ein Filter 2. Ordnung ohne weitere Bauelemente im Sperrbereich doch mit 12 db/Oktave HP=steigen oder TP=fallen sollte. Was es aber nicht tut, wie in meinem Betrag #24 zu sehen.
Die Verluste lt. Schaltbild sind ja Eigenschaft des Bauteiles selbst und so kann man den Verbindungspunkt der Bauteile lt, folgendem Bild nicht erreichen. Bei theoretischer Einführung dieser Punkte A und B stellt sich dann das Verhalten 2. Ordnung wie man es kennt ein und auch der Phasenverlauf geht über 180°.

Zum Vergleich sind auch noch die Verläufe wie im Beitrag #24 enthalten. Ich habe, da ich ja aus der Praxis komme, viel gelernt, danke nochmals.
Freundl. Grüße R.D.
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Asymptotische Steigung und Zahl der Energiespeicher

Die Bode-Diagramme in Post #24 sehen zwar (auf den ersten Blick) aus, als seien es TP bzw. HP zweiter Ordnung mit (sehr) geringer Dämpfung und daher großer Resonanzüberhöhung. Tatsächlich handelt es sich in beiden Fällen um Schwingkreise, wie aus den Schaltbildern, aber auch den asymptotischen Steigungen im Bode-Diagramm zu erkennen ist. Daher ist die Überschrift in Post #25 nicht korrekt. Manchmal lohnt sich also ein zweiter Blick auf eine Problemstellung.
Hier nun ein Bode-Diagramm eines TP 2. Ordnung.

Hieraus ist zu sehen, daß
- die Steigung - 40 dB/Dekade (-12dB/Oktave) beträgt.
- die Phase asymptotisch gegen - 1800 geht.
- die Steilheit des Phasenverlaufs mit fallender Dämpfung größer wird.
Die Steigung und die Zahl der Energie-Speicher
Wie aus dem Bode-Diagramm in Post #26 zu sehen ist, kommen als (asymptotische) Steigungen nur die Werte 0dB/Dekade, ±20dB/Dekade, ±40dB/Dekade (usw.) vor. Das ist bei Netzwerken aus konzentrierten Schaltelementen (R, L, C) grundsätzlich so. Als "Energiespeicher" gelten dabei "L" und "C".
Ob nun aber die (asymptotische) Steigung positiv oder negativ wird, hängt von der Schaltung ab.
- Der RLC Tiefpß
Dieser enthält 2 Energiespeicher, nämlich L und C. Und, wie aus dem Bode-Diagramm zu sehen ist, wird die asymptotische Steigung - 40dB/Dekade.
Beim RLC Hochpaß verhält es sich analog dazu und man erhält eine Steigung von + 40dB/Dekade.
Ist die Aussage: "2 Energiespeicher ergeben eine Steigung von + 40dB/Dekade oder - 40dB/Dekade" so allgemein gültig? Zunächst offensichtlich nur, wenn es sich um einen HP oder einen TP handelt.
- Der LC Schwingkreis
Dieser enthält auch 2 Energiespeicher. "Normalerweise" interessiert dabei nur die Resonanz-Überhöhung (in Abhängigkeit von der Dämpfung). Aber wie verhält es sich mit den (asymptotischen) Steigungen?

Aus Fig. 30 wird erkennbar, daß unabhängig von der Resonanz-Überhöhung, die Durchlaß-Kurven asymptotisch zu beiden Seiten der Resonanzfrequenz einen identischen Verlauf haben. Fig. 30 ist eine lineare Darstellung und kein Bode-Diagramm. In einem Bode-Diagramm wäre zu erkennen, daß die asymptotischen Steigungen + 20 dB/Dekade (für tiefe Frequenzen) und - 20 dB/Dekade (für hohe Frequenzen) betragen.
Bei einem LC-Schwingkreis werden also die asymptotischen Steigungen "aufgeteilt". Aber betragsmäßig zu jeweils 20 dB/Dekade.
- Der RC-Spannungsteiler
Der RC-Spannungsteiler hat auch 2 Energiespeicher. In diesem Fall zwei Kondensatoren.

Als technische Anwendung kommt er bei einer Tastspitze für Oszilloskope vor.

Wie aber sieht es hier mit der asymptotischen Steigung im Frequenzbereich aus? Es ist bekannt, daß sich dieser Spannungsteiler je nach Abgleich entweder als TP oder als HP oder (richtig abgeglichen) frequenzunabhängig verhält.
Offensichtlich gilt hier nicht, daß jeder Energiespeicher asymptotisch 20 dB/Dekade Steigung ergibt. Der Grund dafür liegt darin, daß den beiden Energiespeichern nicht unabhängig von einander eine Anfangsbedingung (hier Spannung am Kondensator zum Zeitpunkt t=0) vorgegeben werden kann. Die beiden Energiespeicher sind somit nicht von einander unabhängig. Man sieht es sofort, wenn man den Eingang als kurz geschlossen ansetzt (ue(t)=0).
Der RC-Spannungsteiler wird imThread "Teiler-Tastkpf an elektronischen Meßgeräten" behandelt.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
Frequenzgrenzen für ausgewogenen Klang

Sowohl beim Telefon, als auch bei Radios mußte das Problem gelöst werden, wie die Frequenzgrenzen zu wählen sind, damit ein ausgewogener Klang entsteht.
"Ausgewogener Klang" ist natürlich eine subjektive Empfindung. Aber es hat sich in der Praxis gezeigt, daß der "normale" Hörer es als ausgewogen empfindet, wenn der geometrische Mittelwert von unterer und oberer Frequenzgrenze zwischen 800 Hz und 1 kHz angesetzt wird.
Für amerikanische Radios gilt gemäß "Kiver, M.: F-M Simplified, van Nostrand, 1947" 800 Hz als geometrischer Mittelwert. Um die Festlegung dieser Grenzen zu vereinfachen, ist dort ein Nomogramm angegeben.

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.
RC gekoppelte Verstärker

In "Boyce, W.F.; Roche, J.J.: Radio Data Book, Boland & Boyce, Inc. Publishers,1948" finden sich für etwa 80 verschiedene US Röhren Beispiele zu RC gekoppelten Verstärkern mit ausführlichen Tabellen für verschiedene Betriebsspannungen und Werten der Schaltelemente.
Folgende Schaltungen werden behandelt:
Trioden Verstärker

Pentoden Verstärker (Batterie-Röhren)

Pentoden Verstärker

Phasen-Umkehrstufe

Durch Vergleich von Daten der Röhren lassen sich auch für hierbei nicht aufgeführte Typen die passenden Tabellen herausfinden. So können die Tabellen dabei helfen, im Fehlerfall Anhaltspunkte dafür zu finden, ob eine gegebene Schaltung (noch) ordnungsgemäß funktioniert.
MfG DR
Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.