Wobbeln: ein Spezialfall der Frequenz-Modulation

In früheren Zeiten mußte man ein Radio mühsam abgleichen, quasi "Punkt für Punkt" mit Hilfe eines (Amplituden modulierbaren) HF-Generators und z.B. eines Röhren-Voltmeters, das die Größe der Ausgangsspannung anzeigen kann.

Seit jedoch Generatoren zur Verfügung stehen, deren Frequenz sich über eine Steuerspannung verändern läßt, sowie Oszilloskope, die die Spannung z.B. am Ende des ZF-Verstärkers darstellen können, hat sich das "Wobbeln" zur Sichtbarmachung seiner Durchlaßkurve und zu dessen Abgleich fast allgemein eingebürgert.

Historisches zum Wobbeln

Strutt [1] beschreibt einen "Frequenzkennlinienschreiber" und zitiert dazu als Schrifttum [118]:
"Mayer, H.F.: A visual alignment generator, Electronics, N.Y. Bd. 13 (1940) Nr. 4, S. 39 -41". 

 

Ardenne [2], der sich schon Ende der 1920er Jahre mit Oszillographenröhren beschäftigt hat und eigene Entwicklungen davon bei Leybold bauen ließ, stellt in seinem Buch (auf S. 311 - 312) eine frühe Wobbelanordnung vor. Da die damaligen Leuchtschirme der Oszillographenröhren noch keine ausreichende Nachleuchtdauer hatten, wurden die Meßkurven photographisch registriert.

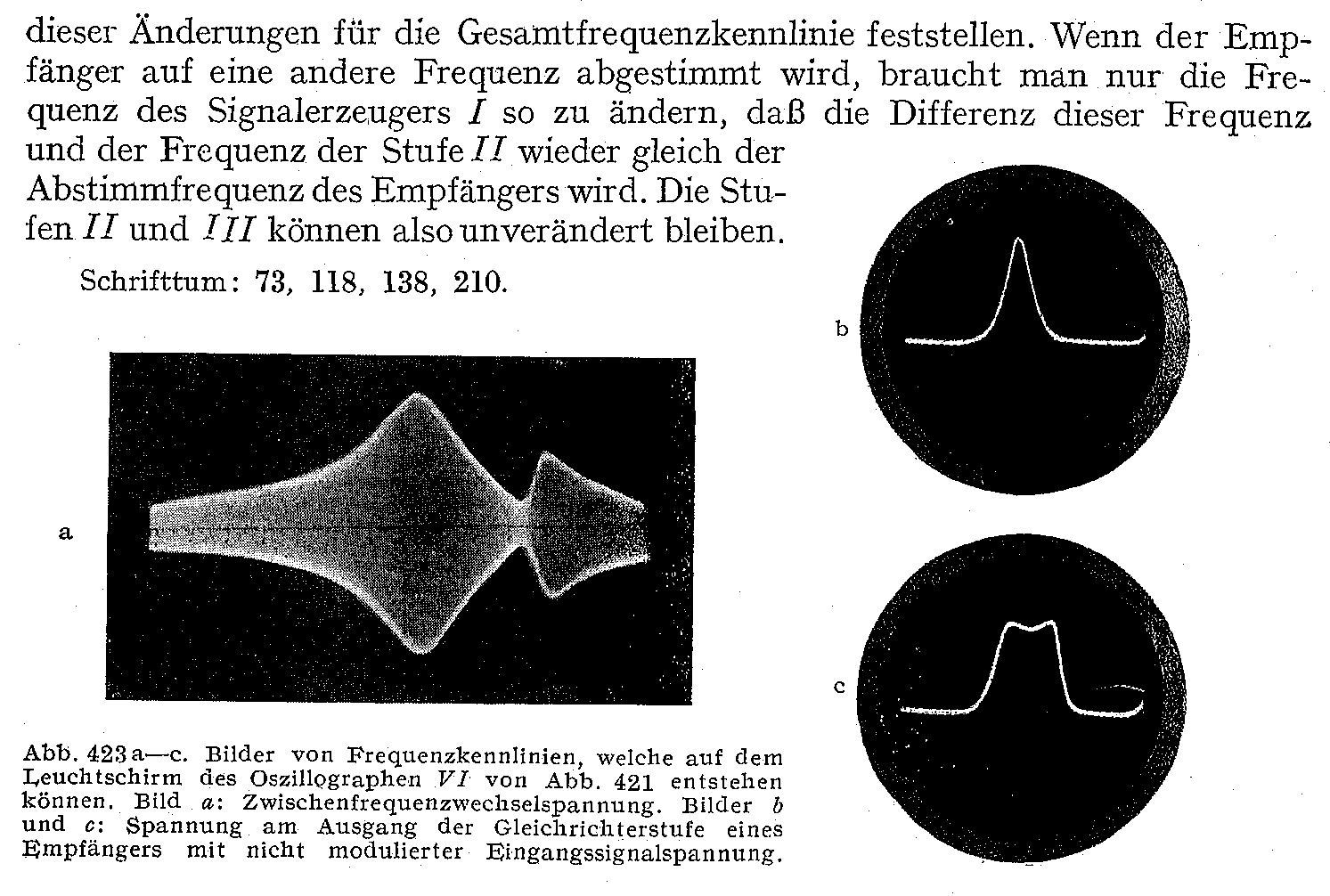
Anstatt, wie bei der Besprechung der Empfängerprüfschaltung angegeben, die Resonanzkurve und die resultierende Niederfrequenzabhängigkeit bei einzelnen Frequenzen, d. h. punktweise aufzunehmen, kommen für präzisere Untersuchungen wieder Methoden mit langsamer Registrierung in Frage. Eine Schaltung zur langsameren Registrierung von Resonanzkurve oder Niederfrequenzabhängigkeit ist in Abb. 349 abgebildet.

Sollen Resonanzkurven registriert werden, so ist es erforderlich, daß die Welle eines Senders stetig in bekannter Gesetzmäßigkeit mit der Zeit geändert wird. Soll die Niederfrequenzabhängigkeit gemessen werden, so ist die Welle eines zweiten Senders, die mit der Welle des Hauptsenders zur Interferenz kommt, stetig zu variieren. Zur Vornahme der Frequenzänderung werden zweckmäßig Tonkondensatoranordnungen benutzt, wie sie schon früher beschrieben wurden (Kapitel C, II, 1, h).

Damit in der Registrierung Amplitudenabhängigkeiten ausgeschaltet sind, soll die Hochfrequenzspannung, die von der veränderlichen Frequenz am Schwingungskreis hervorgerufen wird, klein sein gegenüber der vom Sender konstanter Frequenz im Schwingungskreis entstehenden Spannung. Eine mit der angedeuteten Anordnung erhaltene Registrierung ist in Abb. 350 abgebildet.

Abb. 350. Registrierte Frequenzkurve eines Audionempfängers bei starker Benachteiligung hoher Frequenzen durch weitgetriebene Entdämpfung des Schwingungskreises.

Hier handelt es sich um die resultierende Frequenzkurve eines Rückkopplungsempfängers bei starker Benachteiligung der Frequenzen über 1000 Hertz durch weitgetriebene Entdämpfung.

Gemäß den nachfolgenden Definitionen entsprechen diese "Frequenzkennlinienschreiber" dem breitbandigen Wobbeln.

Breitbandiges - Selektives Wobbeln

Beim Wobbeln unterscheidet man zwischen breitbandigem Wobbeln und selektivem Wobbeln. Dieser Unterschied besteht dabei in der "Anzeige-Einheit", nicht im Wobbel-Generator.

Einspeisen des Senders in das Meßobjekt

Der (Wobbel-) Sender muß äußerst lose (also schwach) an das Meßobjekt - den "Prüfling" - angekoppelt werden. Oft geschieht das mit Hilfe einer "Aufblas-Kappe".

Das Foto zeigt eine solche Aufblas-Kappe, die für Noval-Röhren geeignet ist.

Der innere Zylinder (mit Längsschlitz) ist mit dem Innenleiter der Zuleitung verbunden. Dann kommt eine Isolierschicht und schließlich der Außenzylinder, der mit dem Außenleiter des Kabels verbunden ist. Wichtig ist, daß der Außenzylinder gut leitend mit der Masse des Empfängers verbunden wird.

Das Signal des Senders wird also über die sehr geringe Kapazität zwischen Innenzylinder und Röhrensystem eingespeist.

 

Nicht in allen Fällen kann (aus mechanischen Gründen) eine Aufblas-Kappe verwendet werden. Aber in jedem Fall ist es wichtig, daß die Ankopplung des Wobbel-Senders an den Prüfling äußerst "lose" (und damit rückwirkungs frei) zu erfolgen hat.

Breitbandiges Wobbeln

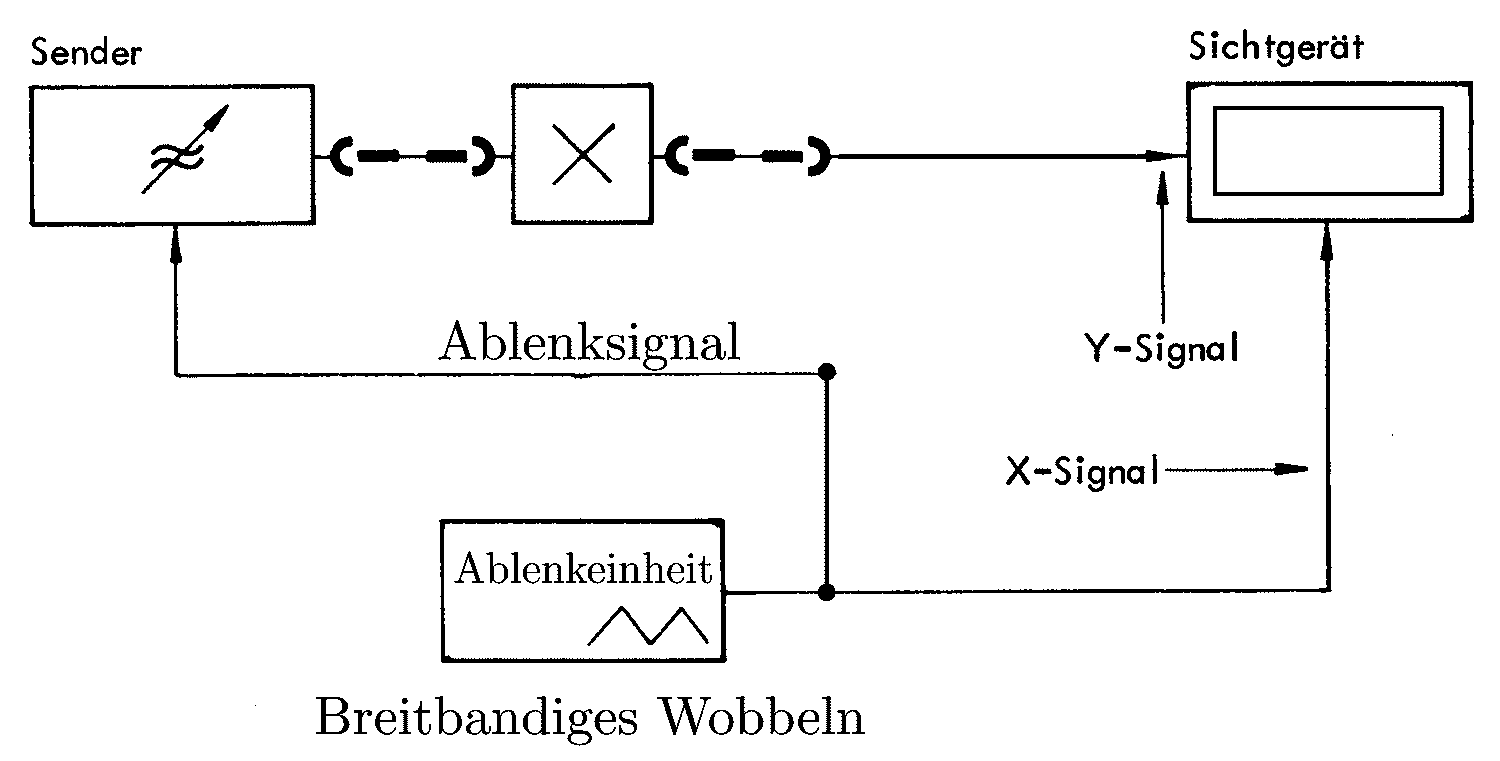
Im nebenstehenden Bild [3] ist das "Sichtgerät" i.a. ein Oszilloskop, das im X/Y Betrieb verwendet wird.

Das Quadrat mit dem "X" stellt den Prüfling dar.

Die Ablenk-Einheit liefert (je nach Typ des Wobbel-Senders) ein Dreieck förmiges, ein Sägezahn  förmiges oder ein Sinus förmiges Ablenksignal.

 

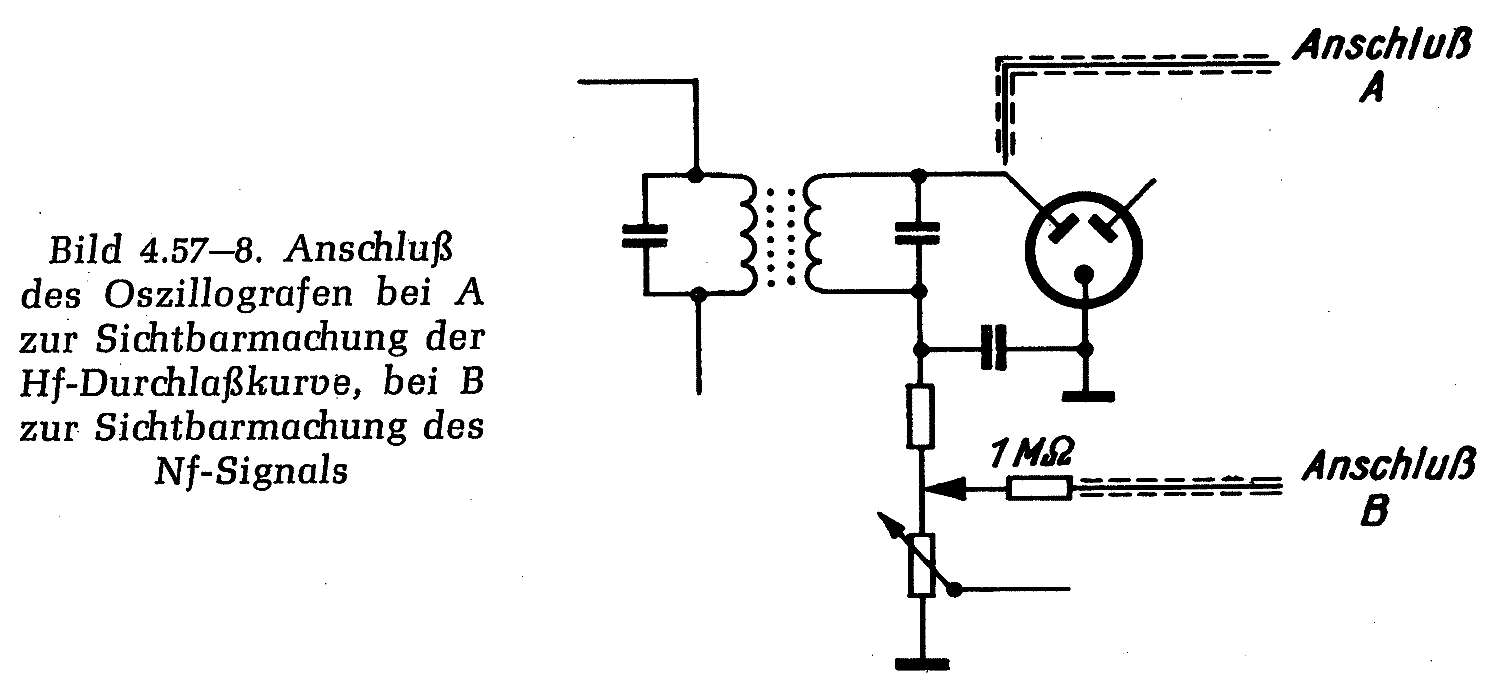Beim Wobbeln eines ZF-Verstärkers (hier als Beispiel ein AM-ZF-Verstärker [4]) kann man das Y-Signal für das Sichtgerät entweder vor der Signal-Diode (Anschluß A) oder nach der Signal-Diode (Anschluß B) abgreifen.

Man erhält dabei unterschiedliche Darstellungen.

 

Messung der HF Spannung

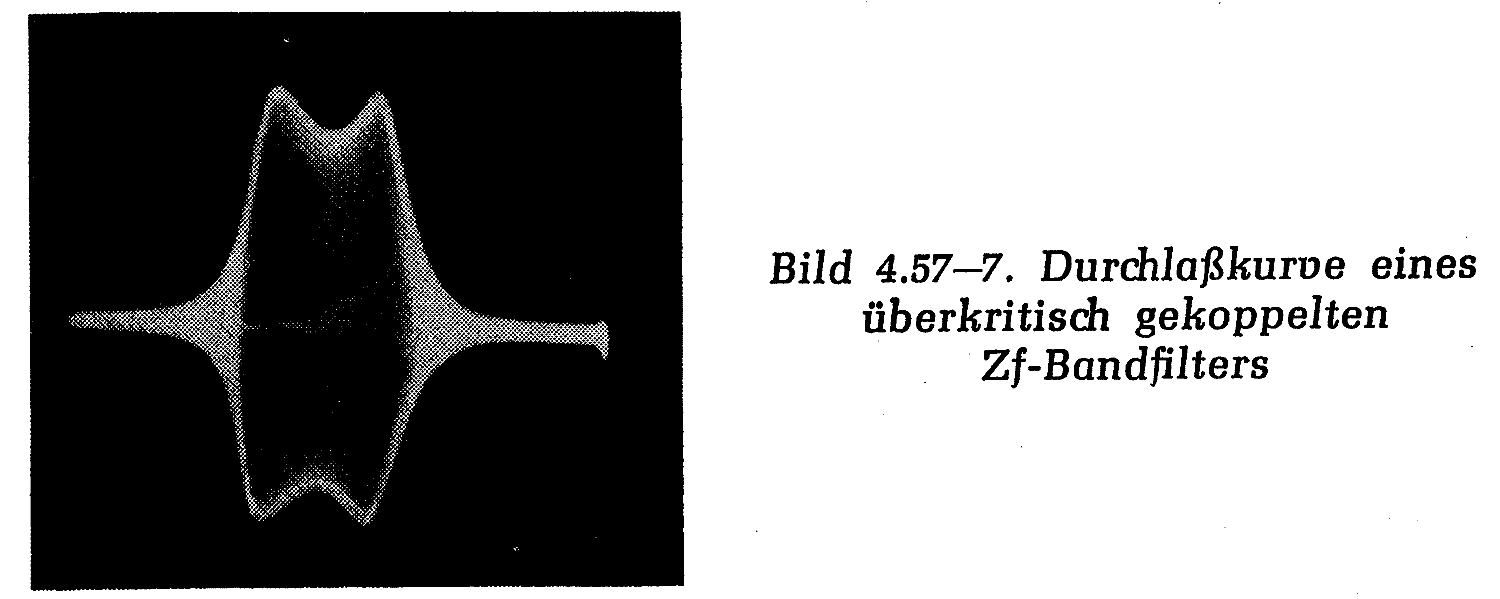Am Anschluß (A) zeigt das Oszilloskop die Ausgangsspannung des ZF-Verstärkers, deren (obere) Hüllkurve dann die Form der Durchlaßkurve hat.[4] Im Prinzip müßte die untere Hüllkurve ein Spiegelbild der oberen sein, ist es im Beispiel aber nicht, weil die Diode den Kreis einseitig belastet. Bei der Messung am Anschluß (A) muß die verwendete Meß-Spitze hochohmig sein, darf also das "Meßobjekt" nicht belasten, z.B. eine 10:1 Tastspitze eines Oszilloskopes.

Messung der gleichgerichteten HF Spannung

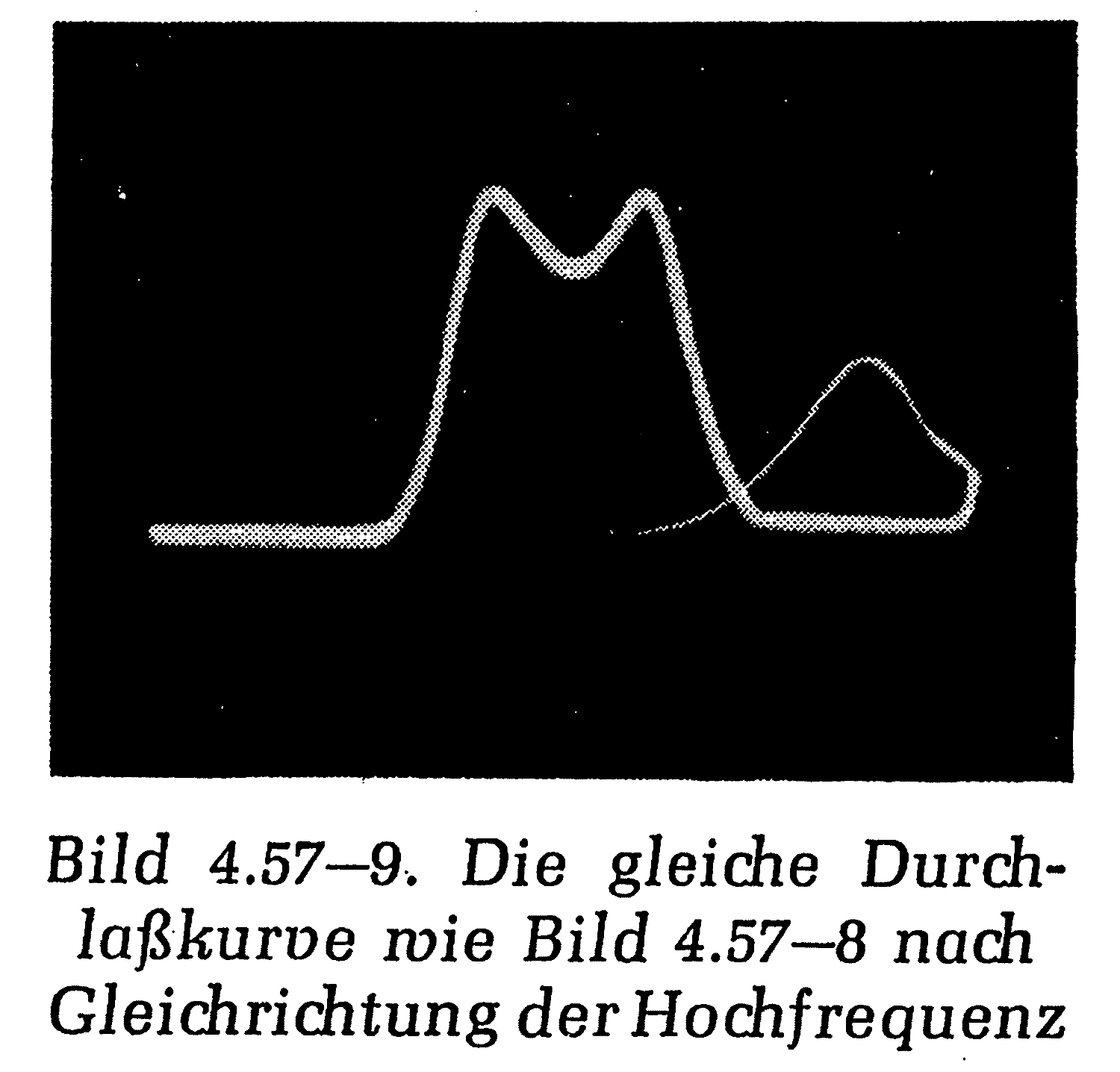
Die Durchlaßkurve des ZF-Verstärkers sieht man dagegen am Anschluß (B). Allerdings geht diese - im Unterschied zu Bild 4.57-9 [4] - nach unten und nicht nach oben. Um die gezeigte Darstellung zu erhalten, muß der Eingang des Oszilloskops auf "invertierend" geschaltet werden.

Auch in diesem Fall muß eine hochohmige Meß-Spitze verwendet werden, wie in der Schaltung Bild 4-57.8 durch den Widerstand von 1 MΩ gezeigt ist.

In der Praxis wird man allerdings einen Tastkopf (des Oszilloskops) mit 10:1 Teiler, also mit 10 MΩ Eingangswiderstand verwenden.

Um Durchlaßkurven entsprechend zu Bild 4.57-9 auch an anderen ZF Stufen (ohne Demodulation mit der Signaldiode, Bild 4.57-8) messen zu können, verwendet man eine Meß-Spitze mit eingebauter Gleichrichter-Diode.

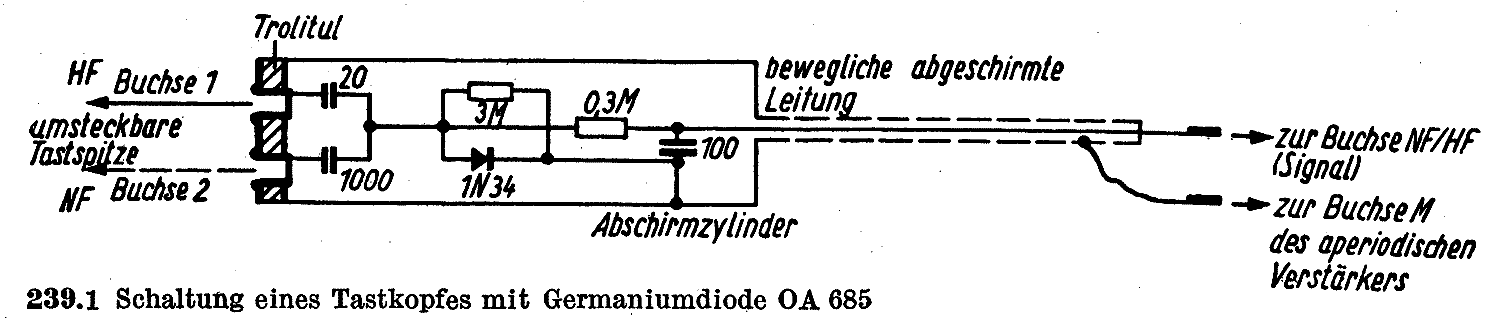
Abb. 239.1 [5] ist ein Vorschlag für eine solche Meß-Spitze. Im Fall der Messung der ZF-Spannung an Punkt (A) ist der Eingang "Buchse 1" zu verwenden. Als Diode ist z.B. eine (hochohmige) Ge Spitzen-Diode zu empfehlen.

Beim Tastkopf Abb. 239.1 kann man eventuell noch einen Kondensator von wenigen pF vor die Buchse 1 in Serie schalten, damit die Belastung der Schaltung durch den Tastkopf noch geringer wird. Auch dieser Tastkopf stellt die Durchlaßkurve Bild 4.57-9 invertiert dar, entsprechend zur Schaltung 4.57-8, Anschluß B.

• Auf Grund der Anlauf- bzw. Knie-Spannungen der Dioden-Kennlinien kann aus den dargestellten Durchlaßkurven der  "-3 dB Punkt" nicht exakt abgelesen werden.

Marker

So simpel, wie bisher dargestellt, waren nur die frühen Wobbler. Man erhielt zwar ein ungefähres Bild der Durchlaßkurve, jedoch war daraus kaum erkennbar, wo die Mittenfrequenz des ZF Verstärkers liegt und welche genaue Bandbreite dieser hat. Darum wurden die Abgleichsender durch Generatoren zur Erzeugung frequenzgenauer Marker ergänzt. Diese Generatoren waren ursprünglich zusätzliche Geräte zum Wobbler, wurden aber später in diese integriert. Bei einigen HF Generatoren ist der Wobbel-Betrieb auch nur auf einigen ZF Frequenzen möglich, z.B. Bereich um 468 kHz oder um 10,7 MHz oder um 5,5 MHz. Die Marker-Generatoren werden dabei aktiviert. Deren Amplitude muß im Vergleich zur Amplitude des Wobbel-Senders klein gewählt werden, so daß die Marken auch nur klein auf der gewobbelten Durchlaßkurve erscheinen.

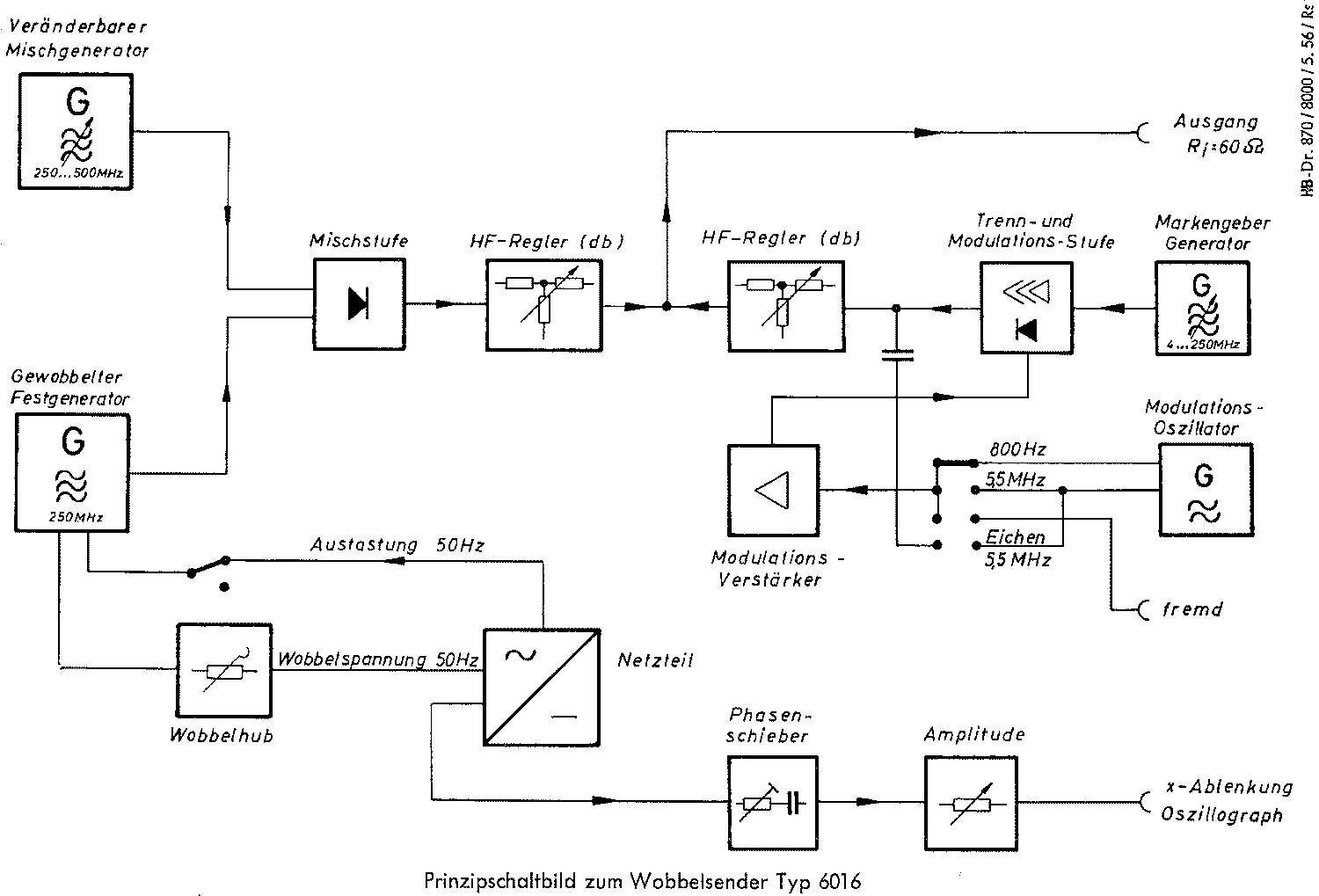
Als Beispiel wird der TV Wobbler Grundig 6016 gewählt.

Das Prinzip-Schaltbild zeigt die Aufbereitung von Wobbelfrequenz, Frequenz-Marken und Ablenkspannung.

 

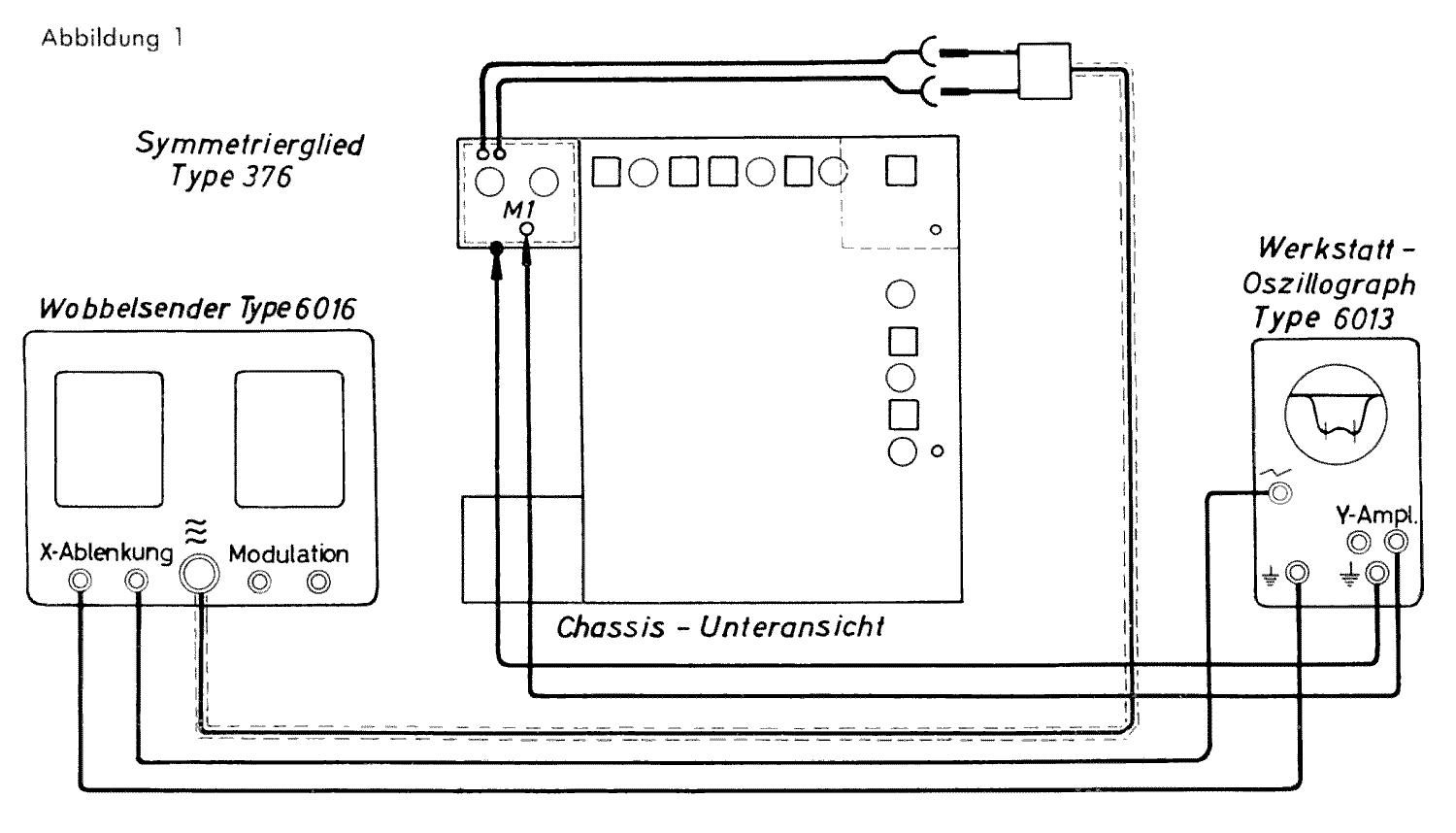
In Abb 1 wird gezeigt, wie die ZF Durchlaßkurve eines (damals noch) Röhren bestückten TV Tuners gewobbelt wird. Man erkennt die beiden Marken als "Piepser" auf der (in negativer Richtung dargestellten) Durchlaßkurve.

Bastelprojekte "Wobbelgenerator"

Im Radiomuseum.org werden verschiedene Bastelprojekte zum Thema "Wobbelgenerator" beschrieben.

• Einfacher Wobbelgenerator mit anlogen IC's
• Generator mit direkter digitaler Synthese der Frequenz (DDS) Beispiel a, Beispiel b, Beispiel c
• Logarithmischer Verstärker für Wobbelsichtgeräte  (Eignet sich auch zur Ergänzung beim Wobbeln mit einem professionellen Wobbelgenerator.)

käufliche DDS Generatoren

Als Beispiel sei der FeelTech FY6600-60M genannt. Diese DDS Generatoren gibt es auch in ähnlicher Art und zu ählichem Preis mit anderer Bezeichnung. Einen Nachteil haben diese Geräte in so fern, als die kleinste einstellbare Ausgangsspannung 1 mV beträgt. Zum Wobbeln eines ZF Verstärkers im Radio empfiehlt es sich, noch einen HF Abschwächer in Serie zum Ausgang zu schalten. Wenn die Durchlaßkurve des Empfängers nur qualitativ (also nur die Form, nicht die genaue Verstärkung) bestimmt werden soll, genügt es als Abschwächung ggf., eine 10:1 Tastspitze an eine isolierte Leitung am Eingang des ZF Verstärkers anzuklemmen.

Selektives Wobbeln

Beim selektiven Wobbeln [3] wird dem Sichtgerät ein selektiver Empfänger vorgeschaltet, der durch das Ablenk-Signal synchron mit dem Wobbel-Sender und dem Sichtgerät abgestimmt wird.

Aufgrund dieser Konfiguration wird immer genau auf der Frequenz ausgewertet, die der Sender gerade erzeugt.

(Beim breitbandigen Wobbeln ist es dagegen auch möglich, auf der Empfangsfrequenz einzuspeisen und auf der Zwischenfrequenz auszuwerten.)

Die Baugruppen "Selektiver Empfänger", "Sichtgerät" und "Ablenkeinheit" stellen zusammen im Prinzip einen Spektrum-Analyser dar.

Ein solcher Spektrum-Analyser hat ein ähnliches Blockschaltbild wie ein typischer Kommunikations-Empfänger. Es handelt sich hier um einen Dreifach-Superhet Empfänger.

Beim Spektrum-Analyser wird der erste lokale Oszillator durch den Sweep-Generator synchron mit der X-Ablenkung des Displays abgestimmt. Als Zeitfunktion des Sweep-Generators wird hier eine (einfacher) Sägezahn-Spannung verwendet. (Der "Rücklauf" des Sägezahns wird unterdrückt.)

Spektrum-Analyser gibt es auch mit eingebautem, synchron mitlaufendem Sender, so daß diese dann als selektives Wobbel-Meßgerät verwendet werden können.

Aufgrund des selektiven Empfangs sind diese Wobbel-Meßgeräte bis zu kleineren Empfangs-Pegeln verwendbar, als es breitbandige Wobbel-Meßgeräte sind.

Wobbeln bei Frequenz-Umsetzung

Viele Wobbelmessungen werden auf einer "Frequenz-Ebene" ausgeführt. Man speist z.B. im Eingang eines ZF Verstärkers ein und mißt an dessen Ausgang.

• Beim breitbandigen Wobbeln kann man auch in der HF Ebene einspeisen und am Ausgang der ZF Ebene messen. Das geht deshalb, weil der Empfangsteil nicht selektiv arbeitet.
• Beim selektiven Wobbeln kann man (i.d.R.) nur in einer Frequenz-Ebene messen, weil sowohl Sender, als auch Empfänger jeweils auf die gleiche Frequenz abgestimmt werden.
  Mit Hilfe eines zusätzlichen Umsetzers kann man aber auch hier "über einen Mischer hinweg" wobbeln.

Ablenk-Zeit beim Wobbeln

Die breitbandigen Wobbler verwenden als Ablenk-Spannung i.a. eine (sinusförmige) 50Hz Wechselspannung, entsprechend zur Netz-Spannung. Und auch bei den selektiven Wobblern wird eine recht niederfrequente Ablenkspannung verwendet, auch wenn es sich um eine Sägezahn-Spannung handelt. 

Was passiert, wenn die Ablenk-Zeit T_sw zu kurz gewählt wird, zeigt nebenstehendes Bild.[6] Das zu wobbelnde System (breitbandiges W.) bzw. das Analyse-Filter des selektiven Empfängers (selektives W.) sind nicht mehr in der Lage, einzuschwingen und erreichen nicht ihre korrekte Amplitude. Statt dessen schwingen sie "nach", also noch immer, obwohl die Frequenz-Linie bereits "weiter gelaufen" ist. (Bei einer Ablenkung durch eine sinus- oder dreieck-förmige Wechselspannung ergäbe sich für den Strahl-Rücklauf zusätzlich eine entsprechend nach links verschobene Kurve.)

Man erkennt aus dieser Graphik ferner, daß die Spektral-Linien nicht als schmale "Delta-Linien", sondern in Form der Durchlaßkurve des "Analyse-Filters" abgebildet werden. 

Das bedeutet auch, daß man dann schneller wobbeln kann, wenn ein breiteres "Analyse-Filter" verwendet wird. Denn je größer die Bandbreite B eines Filters ist, um so schneller kann dieses einschwingen. Die minimal erforderliche Ablenkzeit ergibt sich zu
T_{sw_min} = K*F_span/(B)² .  F_span ist der beim Wobbeln überstrichene Frequenzbereich. K » 1 ist ein Faktor, dessen Größe von der Güte des Filters und dessen Flankensteilheit abhängt.[6]

• Bei den "einfachen" Wobblern ist man mit 50 Hz Ablenkfrequenz auf der "sicheren Seite" beim Wobbeln von FM ZF Verstärkern (5,5 MHz bzw. 10,7 MHz).
• Bei Wobblern für AM ZF Verstärker (120 kHz, 468 kHz) sind Ablenkfrequenzen von < 20 Hz nötig, eventuell aber auch noch weniger, wenn die Filter steile Flanken haben. (Man erniedrigt die Ablenkfrequenz f_ab so lange, bis sich dadurch die dargestellte Kurvenform nicht mehr ändert.)
• Spektrum-Analysatoren als Wobbler wählen die Ablenkgeschwindigkeit eintsprechend zur Breite des Wobbelbereichs automatisch richtig.
   
• Wobbeln funktioniert nur dann richtig, wenn die Ablenkzeit T_sw ausreichend groß gewählt wird, bzw. wenn die Ablenkfrequenz f_ab ausreichend niedrig ist.

Amplitude der Spannung des Wobbelsenders

Die Amplituden der Spannungen, die Wobbel-Sender abgeben können, liegen im Bereich von einigen μV bis mV. Das hat folgende Gründe.

• Beim Wobbeln von AM ZF Verstärkern dürfen diese (noch) nicht durch die automatische Regelspannung in ihrer Verstärkung reduziert werden. (Notfalls feste Regelspannung durch Batterie etc. erzeugen.) Wird das nicht beachtet, mißt man viel zu breite Durchlaß-Kurven.
• Beim Wobbeln von FM ZF Verstärkern darf die letzte (Begrenzer-) Verstärkerstufe, hinter der gemessen wird, eben gerade noch nicht "in die Begrenzung gehen". Auch hier würde man viel zu breite Durchlaß-Kurven messen, wenn bereits eine Amplituden-Begrenzung stattfände.
  Da die HF Spannung der letzten FM ZF Stufe klein sein muß, damit keine Begrenzung stattfindet, ist dann möglicherweise das (gleichgerichtete) Signal des Tastkopfes zu gering, um auf dem Oszilloskop (deutlich) sichtbar zu sein. Abhilfe schafft ein DC Verstärker (z.B. mit einem Operationsverstärker), der dann dem Oszilloskop vorgeschaltet wird und das Ausgangs-Signal des Tastkopfes entsprechend verstärkt.

 

Zusammenhang Wobbeln - Frequenzmodulation

Ein Sender, dassen Frequenz mit Hilfe einer Signalspannung variiert wird, erzeugt eine Frequenzmodulation. Genau dieser Fall liegt ja auch beim Wobbeln vor, nur daß die Signalspannung da entweder nur rein sinusförmig, oder auch sägezahnförmig ist.

• Wie aber muß man sich das unter dem Blickwinkel "Frequenzmodulation" vorstellen?

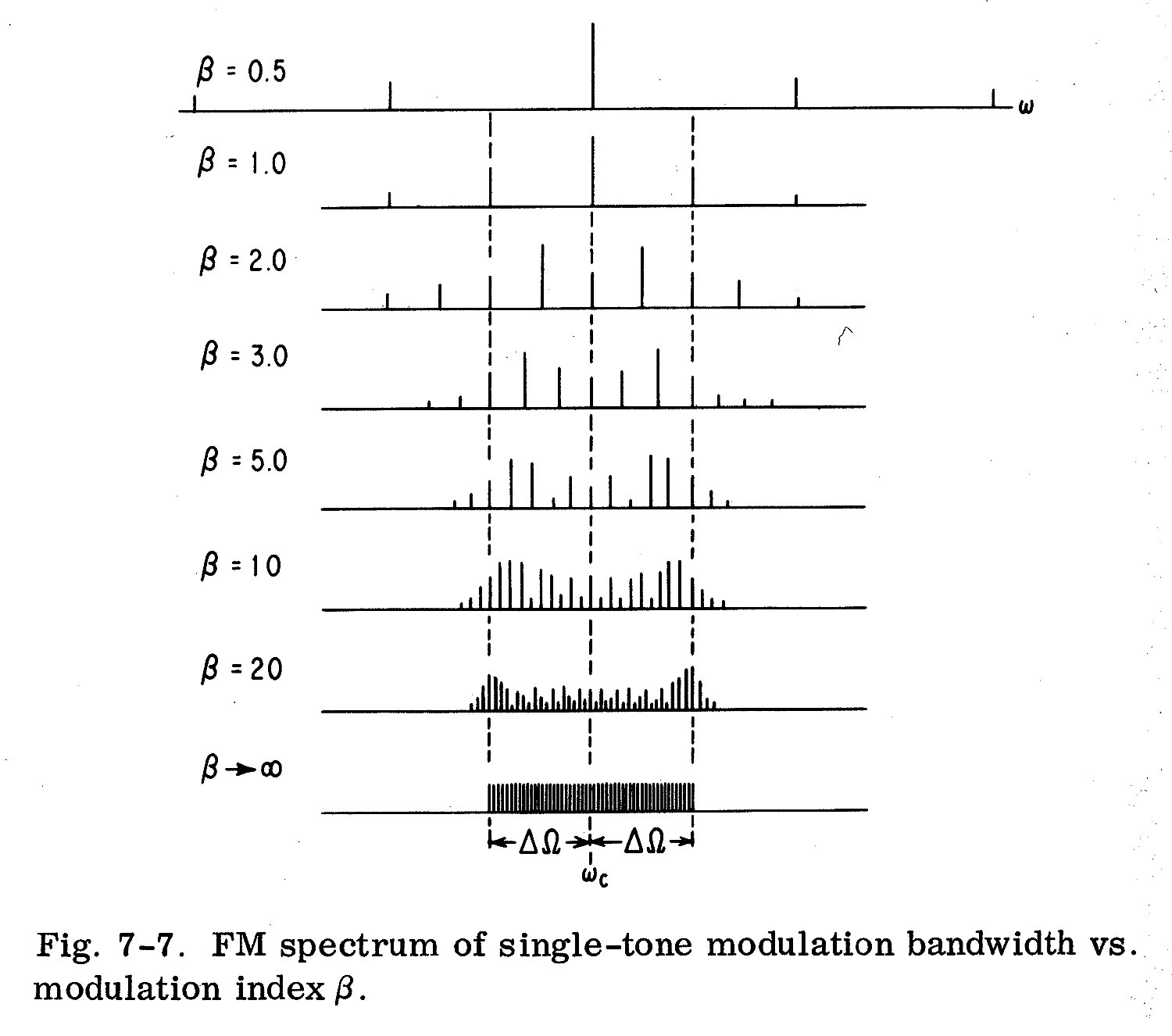
Das Spektrum einer FM Schwingung [7] ist nur für Spezialfälle mathematisch exakt darstellbar. Solch ein Spezialfall ist gerade sinus- bzw. cosinus-förmige Signalspannung bzw. "Ablenkspannung" beim Wobbeln. Man verwendet zur Darstellung Bessel'sche Funktionen und erhält eine spektrale Darstellung gemäß Fig. 7-7 - in Abhängigkeit von der Frequenz der cosinus- bzw. sinus-förmigen Ablenkspannung, bei konstanter Amplitude derselben. 

Der Modulations-Index der FM ist β = ΔΩ/ω_N, wobei ω_N die (Kreis-) Frequenz der Ablenkspannung ist.

Wenn nun ω_N  => 0  geht, wird folglich β ⇒ ∞ gehen. Das entspricht in Fig. 7-7 [8] dem untersten Spektrum. 

Wenn aber die Frequenz der Ablenkspannung sehr klein wird ("theoretisch" gegen 0 geht), hat man doch den oben beschriebenen Fall des Wobbelns.

Die Spektraldarstellung bei FM, Fig 7-7, mit β ⇒ ∞  ist nun aber anscheinend widersprüchlich zu der "hin und her  wandernden Spektrallinie", die man oben beim Wobbeln hatte.

Wie erklärt sich dieser Widerspruch?

• Der (anscheinende) Widerspruch erklärt sich mit der Einschwing-Zeit des Analyse-Filters.

Die Linien im Bessel-Spektrum, Fig. 7-7, sind (theoretisch) unendlich schmal, existieren somit nur bei ganz scharf definierten einzelnen Frequenzen. Bei der praktischen Messung des FM-Spektrums hat man aber stets endlich breite Analyse-Filter, siehe Bild weiter oben, die dann auch noch einschwingen müssen, um auf maximale Amplitude zu kommen. Das können sie aber nur bei entsprechend kleiner Ablenk-Frequenz.

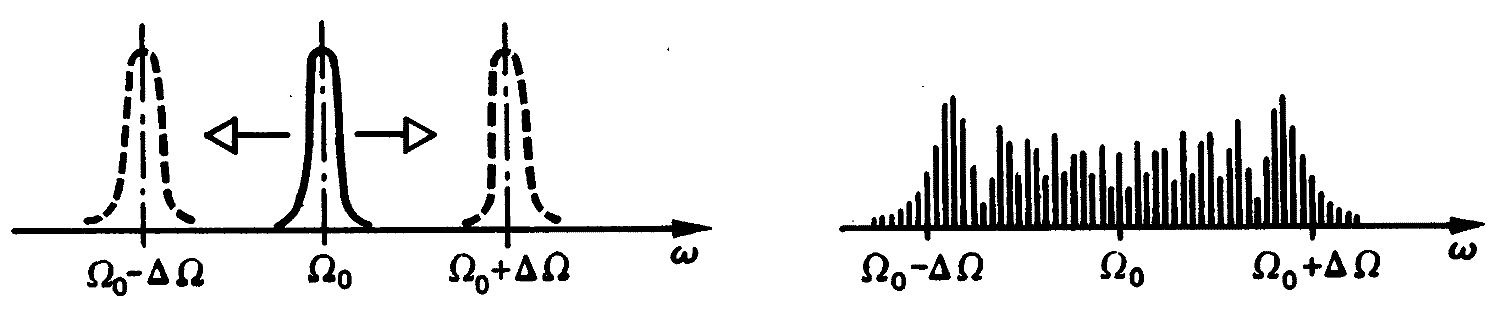
Bild 5.1: Praktisch gemessenes und theoretisches Spektrum einer FM–Schwingung für sehr niederfrequentes Nachrichtensignal

Die Figur (Bild 5.1) zeigt links die "wandernde Spektral-Linie" (in der Form der Durchlaßkurve des Analyse-Filters) und rechts das (theoretische) Bessel-Spektrum, das nur dann so gemessen werden könnte, wenn sich entsprechend schmale Filter-Bandbreiten (mit Filtern entsprechend hoher Güten) realisieren ließen. Zusätzlich würde diese Messung dann entsprechend lange dauern, weil derart schmale Filter entsprechend lange einschwingen müssen.

Messung des FM–Spektrums

 
Damit das von einem Spektrum–Analyzer angezeigte Bild als Spektrum interpretiert werden kann, muß das Analysefilter des Analyzers eingeschwungen sein. Daher muß die Ablenkfrequenz ω_ab umso kleiner sein, je schmaler dieses Filter ist. Die dargestellten Linien sind ein Abbild der Durchlaßkurve dieses Analysefilters. Bei der Messung von FM–Spektren müssen folgende Fälle unterschieden werden. [7]

1. Nachrichtenfrequenz < Ablenkfrequenz : (entspricht dem Wobbeln)

Pro Durchlauf des Analyse–Vorgangs hat sich die Frequenz der FM–Schwingung nur unwesentlich geändert. Das bedeutet, daß dadurch auf dem Schirm eine langsam wandernde Linie sichtbar wird.

• Diese läuft im Bereich Ω₀ − ∆Ω ≤ ω ≤ Ω₀ + ∆Ω hin und her. Dies entspricht dem Wobbelbetrieb.

Gemäß der asymptotischen Bestimmung des FM–Spektrums oder mit Hilfe der Besselfunktionen mit β → ∞ müßte eigentlich so etwas wie eine gleichmäßige Spektralbelegung angezeigt werden, Bild 7-7.

Der Unterschied kommt dadurch zustande, daß die theoretische Breite des Analysefilters B → 0 ist, die praktische jedoch nicht, wodurch ein schnelleres Ein– und Ausschwingen des Filters erfolgt.

2. Nachrichtenfrequenz > Ablenkfrequenz : (entspricht dem FM Bessel-Spektrum)

Das Analysefilter hat in diesem Fall keine Zeit mehr um einzuschwingen, wenn die Momentanfrequenz "vorbeikommt“. Es kann deshalb nicht an jeder Stelle innerhalb ±∆Ω eine Linie abgebildet werden. Jedoch ist bei einer solchen Messung die frequenzmodulierte Zeitfunktion periodisch und damit das Spektrum linienförmig. Jede dieser Linien stellt eine harmonische Teilschwingung dar, die beliebig lange dauert. Daher spielt hierfür die Einschwingzeit keine Rolle mehr. Der Analyzer zeigt deshalb diese Linien, die dem Besselspektrum entsprechen.

3. Nachrichtenfrequenz ∼ Ablenkfrequenz :

In diesem Übergangsgebiet zeigt der Analyzer ein sehr pauschales Bild des Spektrums, das i.a. nur schwer zu interpretieren ist. Im Grunde ist es ein Mischmasch aus Kontinuum, welches mit z.T. wandernden Linien durchsetzt ist. Abhilfe schafft eine anders eingestellte Ablenkfrequenz ω_ab .

Einige Ablenkspannungen und deren Bessel-Spektren

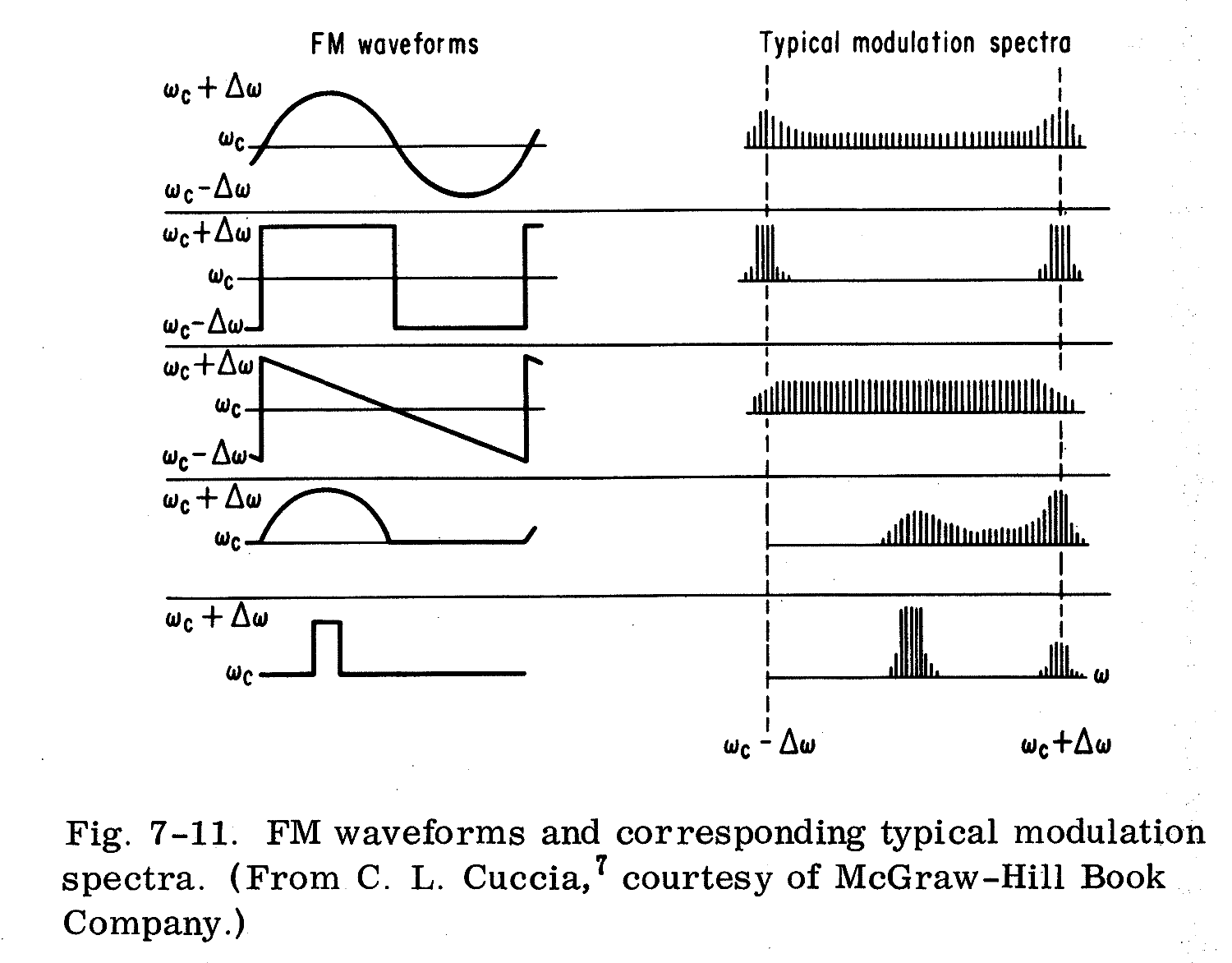Fig. 7-11 [8] zeigt typische Kurvenformen von Ablenkspannungen.

Wie daraus erkennbar wird, ist der Sägezahn für den Fall des Wobbelns besser geeignet als der Sinus bzw. Cosinus. Bei diesem wird zwar die Linie (in Form der Durchlaßkurve des Filters) an den Grenzen des Wobbel-Bereichs nicht größer, aber diese harrt dort länger aus als zwischendrin, was sich in der Darstellung Fig. 7-11 als "Überhöhung" beim typischen Modulations-Spektrum zeigt.

 

[1] Strutt, M.J.O.: Verstärker und Empfänger; Bd. 4 Lehrbuch der Drahtlosen Nachrichtentechnik, 1. A., S. 364, Springer, 1943 (Scan ist aus 2.A. S. 398 & S399, 1951)

[2] v.Ardenne, M.: Die Kathodenstrahlröhre und ihre Anwendung in der Schwachstromtechnik, Springer, 1933

[3] Wandel & Goltermann: Meßmethoden in der Nachrichtenübertragungstechnik, 1978

[4] Renardy, A.: Radio-Service Handbuch, 4.A., Franzis, 1967

[5] Pabst, B.: Anleitung zur Fehlersuche für Rundfunkmechaniker, Teubner, 1961

[6] Anwendungen der Fourier-Transformation (Teil 1)

[7] Frequenz-Modulation

[8] Panter, P. F.: Modulation, Noise, and Spectral Analysis, Mc-Graw-Hill, 1965

---

Den Kollegen Giese, Knoll und Steinmetz danke ich für Anregungen und Ergänzungen.

 

Für diesen Post bedanken, weil hilfreich und/oder fachlich fundiert.